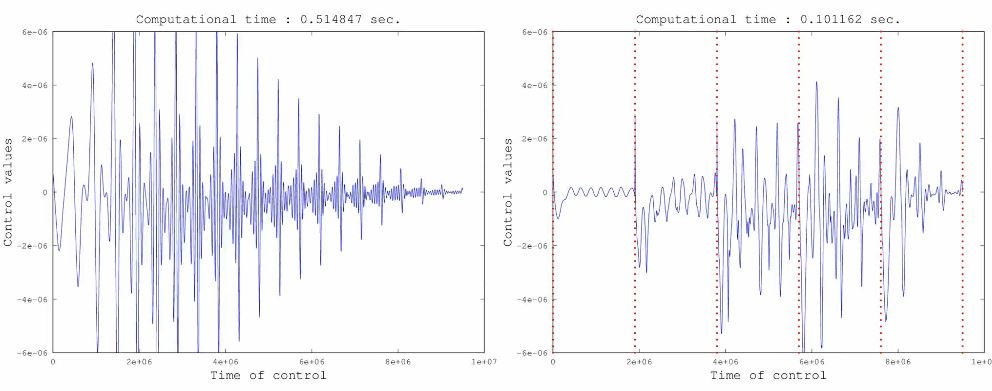
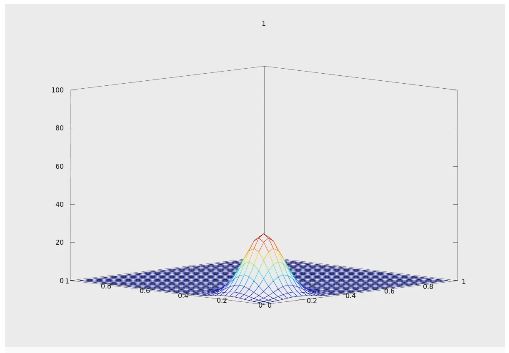
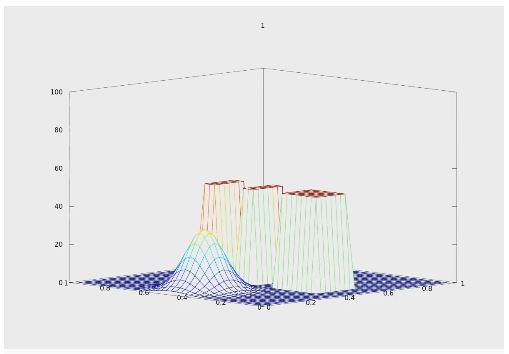
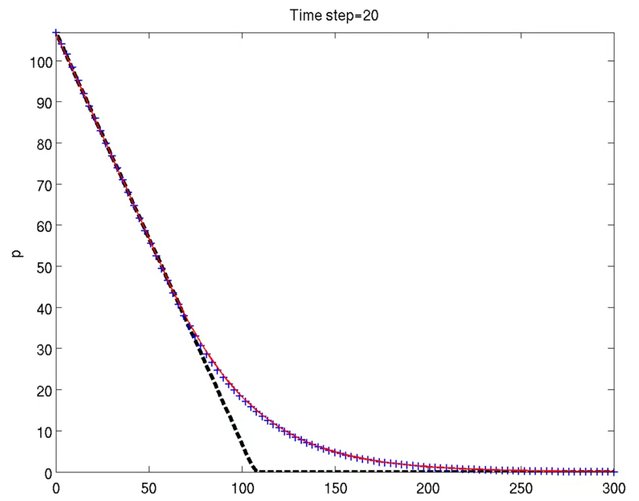
1. Optimal molecular alignment and orientation through rotational ladder climbing
J. Salomon, C. Dion, G. Turinici
The Journal Of Chemical Physics (2005)
@article{ ISI:000232532000030,
Author = {Salomon, J and Dion, CM and Turinici, G},
Title = {{Optimal molecular alignment and orientation through rotational ladder climbing}},
Journal = {{Journal Of Chemical Physics}},
Year = {{2005}},
Volume = {{123}},
Number = {{14}},
Month = {{OCT 8}},
Abstract = {{We study the control by electromagnetic fields of molecular alignment and orientation in a linear, rigid-rotor model. With the help of a monotonically convergent algorithm, we find that the optimal field is in the microwave part of the spectrum and acts by resonantly exciting the rotation of the molecule progressively from the ground state, i.e., by rotational ladder climbing. This mechanism is present not only when maximizing orientation or alignment, but also when using prescribed target states that simultaneously optimize the efficiency of orientation/alignment and its duration. The extension of the optimization method to consider a finite rotational temperature is also presented. (c) 2005 American Institute of Physics.}},
DOI = {{10.1063/1.2049270}},
Article-Number = {{144310}},
ISSN = {{0021-9606}},
ORCID-Numbers = {{TURINICI, Gabriel/0000-0003-2713-006X Dion, Claude/0000-0003-3096-1972}},
Unique-ID = {{ISI:000232532000030}},
}
2. Monotonic time-discretized schemes in quantum control
Y. Maday, J. Salomon, G. Turinici
Numerische Mathematik (2006)
@article{ ISI:000236499500007,
Author = {Maday, Y and Salomon, J and Turinici, G},
Title = {{Monotonic time-discretized schemes in quantum control}},
Journal = {{NUMERISCHE MATHEMATIK}},
Year = {{2006}},
Volume = {{103}},
Number = {{2}},
Pages = {{323-338}},
Month = {{APR}},
Abstract = {{Most of the numerical simulations in quantum (bilinear) control have used monotonically convergent algorithms of Krotov (introduced by Tannor et al. {[}15]), of Zhu \& Rabitz {[}16] or their unified formulation in {[}17]. However, the properties of the discrete version of these procedures have not been yet tackled with. We present in this paper a stable time and space discretization which preserves the monotonic properties of the monotonic algorithms. Numerical results show that the newly derived algorithms are stable and enable various experimentations.}},
DOI = {{10.1007/s00211-006-0678-x}},
ISSN = {{0029-599X}},
ORCID-Numbers = {{TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000236499500007}},
}
3. On the relationship between the local tracking procedures and monotonic schemes in quantum optimal control
J. Salomon, G. Turinici
The Journal Of Chemical Physics (2006)
@article{ ISI:000235473500004,
Author = {Salomon, J and Turinici, G},
Title = {{On the relationship between the local tracking procedures and monotonic schemes in quantum optimal control}},
Journal = {{JOURNAL OF CHEMICAL PHYSICS}},
Year = {{2006}},
Volume = {{124}},
Number = {{7}},
Month = {{FEB 21}},
Abstract = {{Numerical simulations of (bilinear) quantum control often rely on either monotonically convergent algorithms or tracking schemes. However, despite their mathematical simplicity, very limited intuitive understanding exists at this time to explain the former type of algorithms. Departing from the usual mathematical formalization, we present in this paper an interpretation of the monotonic algorithms as finite horizon, local in time, tracking schemes. Our purpose is not to present a new class of procedures but rather to introduce the necessary rigorous framework that supports this interpretation. As a by-product we show that at each instant, estimates of the future quality of the current control field are available and used in the optimization. When the target is expressed as reaching a prescribed final state, we also present an intuitive geometrical interpretation as the minimization of the distance between two correlated trajectories: one starting from the given initial state and the other backward in time from the target state. As an illustration, a stochastic monotonic algorithm is introduced. Numerical discretizations of the two procedures are also presented. (c) 2006 American Institute of Physics.}},
DOI = {{10.1063/1.2170085}},
Article-Number = {{074102}},
ISSN = {{0021-9606}},
Unique-ID = {{ISI:000235473500004}},
}
4. Monotonic Parareal Control for Quantum Systems,
Y. Maday, J. Salomon, G. Turinici
SIAM Journal On Numerical Analysis (2007)
@article{ ISI:000253017000009,
Author = {Maday, Yvon and Salomon, Julien and Turinici, Gabriel},
Title = {{Monotonic parareal control for quantum systems}},
Journal = {{SIAM JOURNAL ON NUMERICAL ANALYSIS}},
Year = {{2007}},
Volume = {{45}},
Number = {{6}},
Pages = {{2468-2482}},
Abstract = {{Following encouraging experimental results in quantum control, numerical simulations have known significant improvements through the introduction of efficient optimization algorithms. Yet, the computational cost still prevents using these procedures for high-dimensional systems often present in quantum chemistry. Using parareal framework, we present here a time parallelization of these schemes which allows us to reduce significantly their computational cost while still finding convenient controls.}},
DOI = {{10.1137/050647086}},
ISSN = {{0036-1429}},
EISSN = {{1095-7170}},
ResearcherID-Numbers = {{Maday, Yvon/C-1397-2013 }},
ORCID-Numbers = {{Maday, Yvon/0000-0002-0443-6544 TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000253017000009}},
}
5. Convergence of the time-discretized monotonic schemes
J. Salomon
M2AN (2007)
@article{ ISI:000246007600004,
Author = {Salomon, Julien},
Title = {{Convergence of the time-discretized monotonic schemes}},
Journal = {{ESAIM-MATHEMATICAL MODELLING AND NUMERICAL ANALYSIS-MODELISATION MATHEMATIQUE ET ANALYSE NUMERIQUE}},
Year = {{2007}},
Volume = {{41}},
Number = {{1}},
Pages = {{77-93}},
Month = {{JAN-FEB}},
Abstract = {{Many numerical simulations in ( bilinear) quantum control use the monotonically convergent Krotov algorithms ( introduced by Tannor et al. {[} Time Dependent Quantum Molecular Dynamics ( 1992) 347 - 360]), Zhu and Rabitz {[} J. Chem. Phys. ( 1998) 385 - 391] or their unified form described in Maday and Turinici {[} J. Chem. Phys. ( 2003) 8191 - 8196]. In Maday et al. {[} Num. Math. ( 2006) 323 - 338], a time discretization which preserves the property of monotonicity has been presented. This paper introduces a proof of the convergence of these schemes and some results regarding their rate of convergence.}},
DOI = {{10.1051/m2an:2007008}},
ISSN = {{0764-583X}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013}},
Unique-ID = {{ISI:000246007600004}},
}
6. Energy conserving algorithms for a co-rotational formulation
J. Salomon, A. Weiss, B. Wohlmuth
SIAM Journal On Numerical Analysis (2008)
@article{ ISI:000256453400009,
Author = {Salomon, J. and Weiss, A. A. and Wohlmuth, B. I.},
Title = {{Energy-conserving algorithms for a corotational formulation}},
Journal = {{SIAM JOURNAL ON NUMERICAL ANALYSIS}},
Year = {{2008}},
Volume = {{46}},
Number = {{4}},
Pages = {{1842-1866}},
Abstract = {{Standard nonlinear schemes for the the simulation of elastodynamic problems have several shortcomings when considering high-speed rotations. To tackle these problems, we use a corotational framework and a corresponding specific linearization to design new energy-conserving numerical schemes. In the two-dimensional case, an algorithm preserving also angular momentum is presented. The existence of a solution for the fully discrete setting of this algorithm is established. Numerical results illustrate the flexibility and efficiency of the proposed algorithms.}},
DOI = {{10.1137/060669863}},
ISSN = {{0036-1429}},
EISSN = {{1095-7170}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013}},
Unique-ID = {{ISI:000256453400009}},
}
7. Formulation and numerical solution of finite-level quantum optimal control problems
A. Borzì, J. Salomon, S. Volkwein
J. Comp. App. Math. (2008)
@article{ ISI:000255424900013,
Author = {Borzi, A. and Salomon, J. and Volkwein, S.},
Title = {{Formulation and numerical solution of finite-level quantum optimal control problems}},
Journal = {{JOURNAL OF COMPUTATIONAL AND APPLIED MATHEMATICS}},
Year = {{2008}},
Volume = {{216}},
Number = {{1}},
Pages = {{170-197}},
Month = {{JUN 15}},
Abstract = {{Optimal control of finite-level quantum systems is investigated, and iterative solution schemes for the optimization of a control representing laser pulses are developed. The purpose of this external field is to channel the system's wavefunction between given states in its most efficient way. Physically motivated constraints, such as limited laser resources or population suppression of certain states, are accounted for through an appropriately chosen cost functional. First-order necessary optimality conditions and second-order sufficient optimality conditions are investigated. For solving the optimal control problems, a cascadic non-linear conjugate gradient scheme and a monotonic scheme are discussed. Results of numerical experiments with a representative finite-level quantum system demonstrate the effectiveness of the optimal control formulation and efficiency and robustness of the proposed approaches. (C) 2007 Elsevier B.V. All rights reserved.}},
DOI = {{10.1016/j.cam.2007.04.029}},
ISSN = {{0377-0427}},
Unique-ID = {{ISI:000255424900013}},
}
8. Energy consistent co-rotational schemes for frictional contact problems
P. Hauret, J. Salomon, A. Weiss, B. Wohlmuth
SIAM Journal On Scientific Computing (2008)
@article{ ISI:000260850000014,
Author = {Hauret, P. and Salomon, J. and Weiss, A. A. and Wohlmuth, B. I.},
Title = {{ENERGY-CONSISTENT COROTATIONAL SCHEMES FOR FRICTIONAL CONTACT PROBLEMS}},
Journal = {{SIAM JOURNAL ON SCIENTIFIC COMPUTING}},
Year = {{2008}},
Volume = {{30}},
Number = {{5}},
Pages = {{2488-2511}},
Abstract = {{In this paper, we consider the unilateral frictional contact problem of a hyperelastic body in the case of large displacements and small strains. In order to retain the linear elasticity framework, we decompose the deformation into a large global rotation and a small elastic displacement. This corotational approach is combined with a primal-dual active set strategy to tackle the contact problem. The resulting algorithm preserves both energy and angular momentum.}},
DOI = {{10.1137/070687827}},
ISSN = {{1064-8275}},
EISSN = {{1095-7197}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013}},
Unique-ID = {{ISI:000260850000014}},
}
9. A stable toolkit method in quantum control
M. Belhadj, J. Salomon, G. Turinici
Journal Of Physics (2008)
@article{ ISI:000258386100001,
Author = {Belhadj, M. and Salomon, J. and Turinici, G.},
Title = {{A stable toolkit method in quantum control}},
Journal = {{JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL}},
Year = {{2008}},
Volume = {{41}},
Number = {{36}},
Month = {{SEP 12}},
Abstract = {{Recently the `toolkit' discretization introduced to accelerate the numerical resolution of the time-dependent Schrodinger equation arising in quantum optimal control problems demonstrated good results on a large range of models. However, when coupling this class of methods with the so-calledmonotonically convergent algorithms, numerical instabilities affect the convergence of the discretized scheme. We present an adaptation of the `toolkit' method which preserves the monotonicity of the procedure. The theoretical properties of the new algorithm are illustrated by numerical simulations.}},
DOI = {{10.1088/1751-8113/41/36/362001}},
Article-Number = {{362001}},
ISSN = {{1751-8113}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013 }},
ORCID-Numbers = {{TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000258386100001}},
}
10. Constructive solution of a bilinear control problem
L. Baudouin, J. Salomon
Systems & Control Letters (2008)
@article{ ISI:000255992800002,
Author = {Baudouin, Lucie and Salomon, Julien},
Title = {{Constructive solution of a bilinear optimal control problem for a Schrodinger equation}},
Journal = {{SYSTEMS \& CONTROL LETTERS}},
Year = {{2008}},
Volume = {{57}},
Number = {{6}},
Pages = {{453-464}},
Month = {{JUN}},
Abstract = {{Often considered in numerical simulations related to the control of quantum systems, the so-called monotonic schemes have not been so far much studied from the functional analysis point of view. Yet, these procedures provide an efficient constructive method for solving a certain class of optimal control problems. This paper aims both at extending the results already available about these algorithms in the finite-dimensional case (i.e., the time-discretized case) and at completing those of the continuous case. This paper starts with some results about the regularity of a functional related to a wide class of models in quantum chemistry. These enable us to extend an inequality due to Lojasiewicz to the infinite-dimensional case. Finally, some inequalities proving the Cauchy character of the monotonic sequence are obtained, followed by an estimation of the rate of convergence. (C) 2007 Elsevier B.V. All rights reserved.}},
DOI = {{10.1016/j.sysconle.2007.11.002}},
ISSN = {{0167-6911}},
EISSN = {{1872-7956}},
Unique-ID = {{ISI:000255992800002}},
}
11. Computation of mean field equilibria in economics
A. Lachapelle, J. Salomon, G. Turinici
M3AS (2010)
@article{ ISI:000280852900003,
Author = {Lachapelle, Aime and Salomon, Julien and Turinici, Gabriel},
Title = {{COMPUTATION OF MEAN FIELD EQUILIBRIA IN ECONOMICS}},
Journal = {{MATHEMATICAL MODELS \& METHODS IN APPLIED SCIENCES}},
Year = {{2010}},
Volume = {{20}},
Number = {{4}},
Pages = {{567-588}},
Month = {{APR}},
Abstract = {{Motivated by a mean field games stylized model for the choice of technologies (with externalities and economy of scale), we consider the associated optimization problem and prove an existence result. To complement the theoretical result, we introduce a monotonic algorithm to find the mean field equilibria. We close with some numerical results, including the multiplicity of equilibria describing the possibility of a technological transition.}},
DOI = {{10.1142/S0218202510004349}},
ISSN = {{0218-2025}},
ORCID-Numbers = {{TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000280852900003}},
}
12. Fast transport optimization on the circle
J. Delon, J. Salomon, A. Sobolevskii
SIAM Journal On Applied Mathematics (2010)
@article{ ISI:000281108800006,
Author = {Delon, Julie and Salomon, Julien and Sobolevski, Andrei},
Title = {{FAST TRANSPORT OPTIMIZATION FOR MONGE COSTS ON THE CIRCLE}},
Journal = {{SIAM JOURNAL ON APPLIED MATHEMATICS}},
Year = {{2010}},
Volume = {{70}},
Number = {{7}},
Pages = {{2239-2258}},
Abstract = {{Consider the problem of optimally matching two measures on the circle, or equivalently two periodic measures on R, and suppose that the cost c(x, y) of matching two points x, y satisfies the Monge condition: c(x(1), y(1)) + c(x(2), y(2)) < c(x(1), y(2)) + c(x(2), y(1)) whenever x(1) < x(2) and y(1) < y(2). We introduce a notion of locally optimal transport plan, motivated by the weak KAM (Aubry-Mather) theory, and show that all locally optimal transport plans are conjugate to shifts and that the cost of a locally optimal transport plan is a convex function of a shift parameter. This theory is applied to a transportation problem arising in image processing: for two sets of point masses on the circle, both of which have the same total mass, find an optimal transport plan with respect to a given cost function c satisfying the Monge condition. In the circular case the sorting strategy fails to provide a unique candidate solution, and a naive approach requires a quadratic number of operations. For the case of N real-valued point masses we present an O(N vertical bar log epsilon vertical bar) algorithm that approximates the optimal cost within epsilon; when all masses are integer multiples of 1/M, the algorithm gives an exact solution in O(N log M) operations.}},
DOI = {{10.1137/090772708}},
ISSN = {{0036-1399}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013 Sobolevski, Andrei/D-9361-2012}},
ORCID-Numbers = {{Sobolevski, Andrei/0000-0002-3082-5113}},
Unique-ID = {{ISI:000281108800006}},
}
13. A smoothing monotonic convergent optimal control algorithm for NMR pulse sequence design
Maximov, J. Salomon, G. Turinici, N. C. Nielsen
The Journal Of Chemical Physics (2010)
@article{ ISI:000275029200010,
Author = {Maximov, Ivan I. and Salomon, Julien and Turinici, Gabriel and Nielsen, Niels Chr.},
Title = {{A smoothing monotonic convergent optimal control algorithm for nuclear magnetic resonance pulse sequence design}},
Journal = {{JOURNAL OF CHEMICAL PHYSICS}},
Year = {{2010}},
Volume = {{132}},
Number = {{8}},
Month = {{FEB 28}},
Abstract = {{The past decade has demonstrated increasing interests in using optimal control based methods within coherent quantum controllable systems. The versatility of such methods has been demonstrated with particular elegance within nuclear magnetic resonance (NMR) where natural separation between coherent and dissipative spin dynamics processes has enabled coherent quantum control over long periods of time to shape the experiment to almost ideal adoption to the spin system and external manipulations. This has led to new design principles as well as powerful new experimental methods within magnetic resonance imaging, liquid-state and solid-state NMR spectroscopy. For this development to continue and expand, it is crucially important to constantly improve the underlying numerical algorithms to provide numerical solutions which are optimally compatible with implementation on current instrumentation and at same time are numerically stable and offer fast monotonic convergence toward the target. Addressing such aims, we here present a smoothing monotonically convergent algorithm for pulse sequence design in magnetic resonance which with improved optimization stability lead to smooth pulse sequence easier to implement experimentally and potentially understand within the analytical framework of modern NMR spectroscopy. (C) 2010 American Institute of Physics. {[}doi:10.1063/1.3328783]}},
DOI = {{10.1063/1.3328783}},
Article-Number = {{084107}},
ISSN = {{0021-9606}},
ResearcherID-Numbers = {{Maximov, Ivan/A-8242-2012 }},
ORCID-Numbers = {{Maximov, Ivan/0000-0001-6319-6774 TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000275029200010}},
}
14. A monotonic method for nonlinear optimal control problems with concave dependence on the state
J. Salomon, G. Turinici
International Journal of Control (2011)
@article{ ISI:000290398400009,
Author = {Salomon, Julien and Turinici, Gabriel},
Title = {{A monotonic method for nonlinear optimal control problems with concave dependence on the state}},
Journal = {{INTERNATIONAL JOURNAL OF CONTROL}},
Year = {{2011}},
Volume = {{84}},
Number = {{3}},
Pages = {{551-562}},
Abstract = {{Initially introduced in the framework of quantum control, the so-called monotonic algorithms have demonstrated very good numerical performance when dealing with bilinear optimal control problems. This article presents a unified formulation that can be applied to more general nonlinear settings compatible with the hypothesis detailed below. In this framework, we show that the well-posedness of the general algorithm is related to a nonlinear evolution equation. We prove the existence of the solution to the evolution equation and give important properties of the optimal control functional. Finally we show how the algorithm works for selected models from the literature. We also compare the algorithm with the gradient algorithm.}},
DOI = {{10.1080/00207179.2011.562548}},
ISSN = {{0020-7179}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013 }},
ORCID-Numbers = {{TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000290398400009}},
}
15. Analysis of the Toolkit method for the time-dependent Schroedinger equation
L. Baudouin, J. Salomon, G. Turinici
Journal of Scientific Computing (2011)
@article{ ISI:000295419200001,
Author = {Baudouin, Lucie and Salomon, Julien and Turinici, Gabriel},
Title = {{Analysis of the ``Toolkit{''} Method for the Time-Dependent Schrodinger Equation}},
Journal = {{JOURNAL OF SCIENTIFIC COMPUTING}},
Year = {{2011}},
Volume = {{49}},
Number = {{2}},
Pages = {{111-136}},
Month = {{NOV}},
Abstract = {{The goal of this paper is to provide an analysis of the ``toolkit{''} method used in the numerical approximation of the time-dependent Schrodinger equation. The ``toolkit{''} method is based on precomputation of elementary propagators and was seen to be very efficient in the optimal control framework. Our analysis shows that this method provides better results than the second order Strang operator splitting. In addition, we present two improvements of the method in the limit of low and large intensity control fields.}},
DOI = {{10.1007/s10915-010-9450-6}},
ISSN = {{0885-7474}},
EISSN = {{1573-7691}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013 }},
ORCID-Numbers = {{TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000295419200001}},
}
16. Time-optimal monotonic convergent algorithms for the control of spin systems
M. Lapert , J. Salomon , D. Sugny
Physical Review A (2012)
@article{ ISI:000301104800004,
Author = {Lapert, M. and Salomon, J. and Sugny, D.},
Title = {{Time-optimal monotonically convergent algorithm with an application to the control of spin systems}},
Journal = {{PHYSICAL REVIEW A}},
Year = {{2012}},
Volume = {{85}},
Number = {{3}},
Month = {{MAR 6}},
Abstract = {{We present a new formulation of monotonically convergent algorithms which allows us to optimize both the control duration and the field fluence. A standard algorithm designs a control field of fixed duration, which both brings the system close to the target state and minimizes its fluence, whereas here we include in addition the optimization of the duration in the cost functional. We apply this new algorithm to the control of spin systems in nuclear magnetic resonance. We show how to implement controlled-NOT gates in systems of two and four coupled spins.}},
DOI = {{10.1103/PhysRevA.85.033406}},
Article-Number = {{033406}},
ISSN = {{1050-2947}},
ResearcherID-Numbers = {{dominique, Sugny/A-3674-2012 salomon, julien/B-3402-2013}},
Unique-ID = {{ISI:000301104800004}},
}
17. Local matching indicators for transport problems with concave costs
J. Delon, J. Salomon, A. Sobolevskii
SIAM Journal on Discrete Mathematics (2012)
@article{ ISI:000305962300026,
Author = {Delon, Julie and Salomon, Julien and Sobolevski, Andrei},
Title = {{LOCAL MATCHING INDICATORS FOR TRANSPORT PROBLEMS WITH CONCAVE COSTS}},
Journal = {{SIAM JOURNAL ON DISCRETE MATHEMATICS}},
Year = {{2012}},
Volume = {{26}},
Number = {{2}},
Pages = {{801-827}},
Abstract = {{In this paper, we introduce a class of local indicators that enable us to compute efficiently optimal transport plans associated with arbitrary weighted distributions of N demands and M supplies in R in the case where the cost function is concave. Indeed, whereas this problem can be solved linearly when the cost is a convex function of the distance on the line (or more generally when the cost matrix between points is a Monge matrix), to the best of our knowledge no simple solution has been proposed for concave costs, which are more realistic in many applications, especially in economic situations. The problem we consider may be unbalanced, in the sense that the weight of all the supplies might be larger than the weight of all the demands. We show how to use the local indicators hierarchically to solve the transportation problem for concave costs on the line.}},
DOI = {{10.1137/110823304}},
ISSN = {{0895-4801}},
EISSN = {{1095-7146}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013 Sobolevski, Andrei/D-9361-2012}},
ORCID-Numbers = {{Sobolevski, Andrei/0000-0002-3082-5113}},
Unique-ID = {{ISI:000305962300026}},
}
18. A Reduced Basis Method for Parametrized Variational Inequalities
B. Haasdonk, J. Salomon, B. Wohlmuth
SIAM Journal On Numerical Analysis (2012)
@article{ ISI:000310329800023,
Author = {Haasdonk, B. and Salomon, J. and Wohlmuth, B.},
Title = {{A REDUCED BASIS METHOD FOR PARAMETRIZED VARIATIONAL INEQUALITIES}},
Journal = {{SIAM JOURNAL ON NUMERICAL ANALYSIS}},
Year = {{2012}},
Volume = {{50}},
Number = {{5}},
Pages = {{2656-2676}},
Abstract = {{Reduced basis methods are an efficient tool for significantly reducing the computational complexity of solving parametrized PDEs. Originally introduced for elliptic equations, they have been generalized during the last decade to various types of elliptic, parabolic, and hyperbolic systems. In this article, we extend the reduction technique to parametrized variational inequalities. First, we propose a reduced basis variational inequality scheme in a saddle point form and prove existence and uniqueness of the solution. We state some elementary analytical properties of the scheme such as reproduction of solutions, a priori stability with respect to the data, and Lipschitz-continuity with respect to the parameters. An offline/online decomposition guarantees an efficient assembling of the reduced scheme, which can be solved by constrained quadratic programming. Second, we provide rigorous a posteriori error bounds with a partial offline/online decomposition. The reduction scheme is applied to one-dimensional obstacle problems. The numerical results confirm the theoretical ones and demonstrate the efficiency of the reduction technique.}},
DOI = {{10.1137/110835372}},
ISSN = {{0036-1429}},
ResearcherID-Numbers = {{salomon, julien/B-3402-2013}},
Unique-ID = {{ISI:000310329800023}},
}
19. Newton algorithm for operator identification in quantum control
M. Ndong, J. Salomon, D. Sugny
Journal of Physics (2014)
@article{ ISI:000338491100009,
Author = {Ndong, M. and Salomon, J. and Sugny, D.},
Title = {{Newton algorithm for Hamiltonian characterization in quantum control}},
Journal = {{JOURNAL OF PHYSICS A-MATHEMATICAL AND THEORETICAL}},
Year = {{2014}},
Volume = {{47}},
Number = {{26}},
Month = {{JUL 4}},
Abstract = {{We propose a Newton algorithm to characterize the Hamiltonian of a quantum system interacting with a given laser field. The algorithm is based on the assumption that the evolution operator of the system is perfectly known at a fixed time. The computational scheme uses the Crank-Nicholson approximation to explicitly determine the derivatives of the propagator with respect to the Hamiltonians of the system. In order to globalize this algorithm, we use a continuation method that improves its convergence properties. This technique is applied to a two-level quantum system and to a molecular one with a double-well potential. The numerical tests show that accurate estimates of the unknown parameters are obtained in some cases. We discuss the numerical limits of the algorithm in terms of the basin of convergence and the non-uniqueness of the solution.}},
DOI = {{10.1088/1751-8113/47/26/265302}},
Article-Number = {{265302}},
ISSN = {{1751-8113}},
EISSN = {{1751-8121}},
Unique-ID = {{ISI:000338491100009}},
}
20. Parareal in time 3D numerical solver for the LWR Benchmark neutron diffusion transient model
A.-M. Baudron, J.-J. Lautard, Y. Maday, K. Riahi, J. Salomon
Journal Of Computational Physics (2014)
@article{ ISI:000342750100005,
Author = {Baudron, Anne-Marie and Lautard, Jean-Jacques and Maday, Yvon and Riahi, Mohamed Kamel and Salomon, Julien},
Title = {{Parareal in time 3D numerical solver for the LWR Benchmark neutron diffusion transient model}},
Journal = {{JOURNAL OF COMPUTATIONAL PHYSICS}},
Year = {{2014}},
Volume = {{279}},
Pages = {{67-79}},
Month = {{DEC 15}},
Abstract = {{In this paper we present a time-parallel algorithm for the 3D neutrons calculation of a transient model in a nuclear reactor core. The neutrons calculation consists in numerically solving the time dependent diffusion approximation equation, which is a simplified transport equation. The numerical resolution is done with finite elements method based on a tetrahedral meshing of the computational domain, representing the reactor core, and time discretization is achieved using a theta-scheme. The transient model presents moving control rods during the time of the reaction. Therefore, cross-sections (piecewise constants) are taken into account by interpolations with respect to the velocity of the control rods. The parallelism across the time is achieved by an adequate use of the parareal in time algorithm to the handled problem. This parallel method is a predictor corrector scheme that iteratively combines the use of two kinds of numerical propagators, one coarse and one fine. Our method is made efficient by means of a coarse solver defined with large time step and fixed position control rods model, while the fine propagator is assumed to be a high order numerical approximation of the full model. The parallel implementation of our method provides a good scalability of the algorithm. Numerical results show the efficiency of the parareal method on large light water reactor transient model corresponding to the Langenbuch-Maurer-Werner benchmark. (C) 2014 Elsevier Inc. All rights reserved.}},
DOI = {{10.1016/j.jcp.2014.08.037}},
ISSN = {{0021-9991}},
EISSN = {{1090-2716}},
ORCID-Numbers = {{RIAHI, Mohamed Kamel/0000-0001-7987-1391}},
Unique-ID = {{ISI:000342750100005}},
}
21. A method for solving exact-controllability problems governed by closed quantum spin systems
A. Borzì, G. Ciaramella, J. Salomon
International Journal of Control (2015)
@article{ ISI:000350449200002,
Author = {Ciaramella, G. and Salomon, J. and Borzi, A.},
Title = {{A method for solving exact-controllability problems governed by closed quantum spin systems}},
Journal = {{INTERNATIONAL JOURNAL OF CONTROL}},
Year = {{2015}},
Volume = {{88}},
Number = {{4}},
Pages = {{682-702}},
Month = {{APR 3}},
Abstract = {{The Liouville-von Neumann master equation models closed quantum spin systems that arise in nuclear magnetic resonance applications. In this paper, an efficient and robust computational framework to solve exact-controllability problems governed by the Liouville-von Neumann master equation is presented. The proposed control framework is based on a new optimisation formulation of exact-controllability quantum spin problems that allows the application of efficient computational techniques. This formulation results in an optimality system with four differential equations and an optimality condition. The differential equations are approximated with an appropriate modified Crank-Nicholson scheme and the resulting discretised optimality system is solved with a matrix-free Krylov-Newton scheme combined with a cascadic nonlinear conjugate gradient initialisation. Results of numerical experiments demonstrate the ability of the proposed framework to solve quantum spin exact-controllability control problems.}},
DOI = {{10.1080/00207179.2014.971435}},
ISSN = {{0020-7179}},
EISSN = {{1366-5820}},
Unique-ID = {{ISI:000350449200002}},
}
22. Ensemble controllability and discrimination of perturbed bilinear control systems on connected, simple, compact Lie groups
M. Belhadj, J. Salomon, G. Turinici
European Journal of Control (2015) Preprint HAL: hal-00866229
@article{ ISI:000351644000004,
Author = {Belhadj, Mohamed and Salomon, Julien and Turinici, Gabriel},
Title = {{Ensemble controllability and discrimination of perturbed bilinear control systems on connected, simple, compact Lie groups}},
Journal = {{EUROPEAN JOURNAL OF CONTROL}},
Year = {{2015}},
Volume = {{22}},
Pages = {{23-29}},
Month = {{MAR}},
Abstract = {{The controllability of bilinear systems is well understood for finite dimensional isolated systems where the control can be implemented exactly. However when perturbations are present some interesting theoretical questions are raised. We consider in this paper a control system whose control cannot be implemented exactly but is shifted by a time independent constant in a discrete list of possibilities. We prove under general hypothesis that the collection of possible systems (one for each possible perturbation) is simultaneously controllable with a common control. The result is extended to the situations where the perturbations are constant over a common, long enough, time frame. We apply the result to the controllability of quantum systems. Furthermore, some examples and a convergence result are presented for the situation where an infinite number of perturbations occurs. In addition, the techniques invoked in the proof allow us to obtain generic necessary and sufficient conditions for ensemble controllability. (C) 2015 European Control Association. Published by Elsevier Ltd. All rights reserved.}},
DOI = {{10.1016/j.ejcon.2014.12.003}},
ISSN = {{0947-3580}},
EISSN = {{1435-5671}},
ORCID-Numbers = {{TURINICI, Gabriel/0000-0003-2713-006X}},
Unique-ID = {{ISI:000351644000004}},
}
23. Reduced basis methods for pricing options with the Black-Scholes and Heston model
O. Burkovska, B. Haasdonk, J. Salomon, B. Wohlmuth
SIAM Journal on Financial Mathematics (2015)
@article{ ISI:000367013000025,
Author = {Burkovska, O. and Haasdonk, B. and Salomon, J. and Wohlmuth, B.},
Title = {{Reduced Basis Methods for Pricing Options with the Black-Scholes and Heston Models}},
Journal = {{SIAM JOURNAL ON FINANCIAL MATHEMATICS}},
Year = {{2015}},
Volume = {{6}},
Number = {{1}},
Pages = {{685-712}},
Abstract = {{In this paper, we present a reduced basis method for pricing European and American options based on the Black-Scholes and Heston models. To tackle each model numerically, we formulate the problem in terms of a time-dependent variational equality or inequality. We apply a suitable reduced basis approach for both types of options. The characteristic ingredients used in the method are a combined POD-Greedy and Angle-Greedy procedure for the construction of the primal and dual reduced spaces. Analytically, we prove the reproduction property of the reduced scheme and derive a posteriori error estimators. Numerical examples are provided, illustrating the approximation quality and convergence of our approach for the different option pricing models. Also, we investigate the reliability and effectivity of the error estimators.}},
DOI = {{10.1137/140981216}},
ISSN = {{1945-497X}},
Unique-ID = {{ISI:000367013000025}},
}
24. Discrete-valued-pulse optimal control algorithms: Application to spin systems
G. Dridi, M. Lapert, J. Salomon, S. J. Glaser, D. Sugny
Physical Review A (2015)
@article{ ISI:000363230800003,
Author = {Dridi, G. and Lapert, M. and Salomon, J. and Glaser, S. J. and Sugny, D.},
Title = {{Discrete-valued-pulse optimal control algorithms: Application to spin systems}},
Journal = {{PHYSICAL REVIEW A}},
Year = {{2015}},
Volume = {{92}},
Number = {{4}},
Month = {{OCT 22}},
Abstract = {{This article is aimed at extending the framework of optimal control techniques to the situation where the control field values are restricted to a finite set. We propose generalizations of the standard GRAPE algorithm suited to this constraint. We test the validity and the efficiency of this approach for the inversion of an inhomogeneous ensemble of spin systems with different offset frequencies. It is shown that a remarkable efficiency can be achieved even for a very limited number of discrete values. Some applications in nuclear magnetic resonance are discussed.}},
DOI = {{10.1103/PhysRevA.92.043417}},
Article-Number = {{043417}},
ISSN = {{2469-9926}},
EISSN = {{2469-9934}},
ResearcherID-Numbers = {{Glaser, Steffen/B-7335-2009}},
ORCID-Numbers = {{Glaser, Steffen/0000-0003-4099-3177}},
Unique-ID = {{ISI:000363230800003}},
}
25. A fully efficient time-parallelized quantum optimal control algorithm
K. M. Riahi, J. Salomon, S. J. Glaser, D. Sugny
Physical Review A (2016)
@article{ ISI:000373872400005,
Author = {Riahi, M. K. and Salomon, J. and Glaser, S. J. and Sugny, D.},
Title = {{Fully efficient time-parallelized quantum optimal control algorithm}},
Journal = {{PHYSICAL REVIEW A}},
Year = {{2016}},
Volume = {{93}},
Number = {{4}},
Month = {{APR 13}},
Abstract = {{We present a time-parallelization method that enables one to accelerate the computation of quantum optimal control algorithms. We show that this approach is approximately fully efficient when based on a gradient method as optimization solver: the computational time is approximately divided by the number of available processors. The control of spin systems, molecular orientation, and Bose-Einstein condensates are used as illustrative examples to highlight the wide range of applications of this numerical scheme.}},
DOI = {{10.1103/PhysRevA.93.043410}},
Article-Number = {{043410}},
ISSN = {{2469-9926}},
EISSN = {{2469-9934}},
ResearcherID-Numbers = {{Glaser, Steffen/B-7335-2009}},
ORCID-Numbers = {{Glaser, Steffen/0000-0003-4099-3177}},
Unique-ID = {{ISI:000373872400005}},
}
26. Optimal periodic control of spin systems: Application to the maximization of the signal to noise ratio per unit time
N. Jbili, K. Hamraoui, S. Glaser, J. Salomon, D. Sugny,
Physical Review A (2019)
@article{ ISI:000468201600008,
Author = {Jbili, N. and Hamraoui, K. and Glaser, S. J. and Salomon, J. and Sugny,
D.},
Title = {{Optimal periodic control of spin systems: Application to the
maximization of the signal-to-noise ratio per unit time}},
Journal = {{PHYSICAL REVIEW A}},
Year = {{2019}},
Volume = {{99}},
Number = {{5}},
Month = {{MAY 15}},
Abstract = {{We propose an optimal control algorithm for periodic spin dynamics. This
nontrivial optimization problem involves the design of a control field
maximizing a figure of merit, while finding the initial and final states
of the dynamics, which are not known but are subjected to specific
periodic conditions. As an illustrative example, we consider the
maximization of the signal-to-noise ratio per unit time of spin systems.
In the case of a homogeneous spin ensemble and a very short control
duration, we show numerically that the optimal field corresponds to the
Ernst angle solution. We investigate the optimal control process for
longer control durations and their sensitivity to offset
inhomogeneities.}},
DOI = {{10.1103/PhysRevA.99.053415}},
Article-Number = {{053415}},
ISSN = {{2469-9926}},
EISSN = {{2469-9934}},
Unique-ID = {{ISI:000468201600008}},
}
27. Methods of Reflections: relations with Schwarz methods and classical stationary iterations, scalability and preconditioning.
G. Ciaramella, M. J. Gander, L Halpern, J. Salomon,
SMAI Journal Of Computational Mathematics (2019)
@article{SMAI-JCM_2019__5__161_0,
author = {Gabriele Ciaramella and Martin J. Gander and Laurence Halpern and Julien Salomon},
title = {Methods of Reflections: relations with Schwarz methods and classical stationary iterations, scalability and preconditioning.},
journal = {The SMAI journal of computational mathematics},
publisher = {Soci\'et\'e de Math\'ematiques Appliqu\'ees et Industrielles},
volume = {5},
year = {2019},
pages = {161-193},
doi = {10.5802/smai-jcm.46},
language = {en},
url={smai-jcm.centre-mersenne.org/item/SMAI-JCM_2019__5__161_0/}
}
28. PARAOPT: A parareal algorithm for optimality systems
M. Gander, F. Kwok, J. Salomon
SIAM Journal on Scientific Computing (2020)
@article{doi:10.1137/19M1292291,
author = {Gander, Martin J. and Kwok, Felix and Salomon, Julien},
title = {PARAOPT: A Parareal Algorithm for Optimality Systems},
journal = {SIAM Journal on Scientific Computing},
volume = {42},
number = {5},
pages = {A2773-A2802},
year = {2020},
doi = {10.1137/19M1292291},
URL = {https://doi.org/10.1137/19M1292291},
eprint = {https://doi.org/10.1137/19M1292291}
}
29. On the method of reflections
P. Laurent, G. Legendre, J. Salomon
Numerische Mathematik (2021)
@article{LLS,
Author = {Laurent, Philippe and Legendre, Guillaume and Salomon, Julien},
Title = {On the method of reflections},
Journal = {NUMERISCHE MATHEMATIK},
Year = {2021},
Volume = {148},
Number = {2},
Pages = {449-493},
Month = {JUN},
DOI = {10.1007/s00211-021-01207-6},
ISSN = {0029-599X},
EISSN = {0945-3245},
Unique-ID = {WOS:000664003700001}
}
30. Optimization of bathymetry for long waves with
small amplitude
P.-H. Cocquet, S. Riffo, J. Salomon
SIAM Journal on Control and Optimization (2021 )
@article{doi:10.1137/20M1326337,
author = {Cocquet, Pierre-Henri and Riffo, Sebastian and Salomon, Julien},
title = {Optimization of Bathymetry for Long Waves with Small Amplitude},
journal = {SIAM Journal on Control and Optimization},
volume = {59},
number = {6},
pages = {4429-4456},
year = {2021},
doi = {10.1137/20M1326337},
URL = {
https://doi.org/10.1137/20M1326337
},
eprint = {
https://doi.org/10.1137/20M1326337
}
}
31. Analysis of the Blade Element Momentum Theory
J. Ledoux, S. Riffo, J. Salomon
SIAM Journal on Applied Mathematics (2021)
@article{doi:10.1137/20M133542X,
author = {Ledoux, Jeremy and Riffo, Sebastián and Salomon, Julien},
title = {Analysis of the Blade Element Momentum Theory},
journal = {SIAM Journal on Applied Mathematics},
volume = {81},
number = {6},
pages = {2596-2621},
year = {2021},
doi = {10.1137/20M133542X},
URL = {
https://doi.org/10.1137/20M133542X
},
eprint = {
https://doi.org/10.1137/20M133542X
}
}
32. Analysis of a Greedy Reconstruction Algorithm
S. Buchwald, G. Ciaramella and J. Salomon
SIAM Journal on Control and Optimization (2021)
@article{doi:10.1137/20M1373384,
author = {Buchwald, S. and Ciaramella, G. and Salomon, J.},
title = {Analysis of a Greedy Reconstruction Algorithm},
journal = {SIAM Journal on Control and Optimization},
volume = {59},
number = {6},
pages = {4511-4537},
year = {2021},
doi = {10.1137/20M1373384},
URL = {
https://doi.org/10.1137/20M1373384
},
eprint = {
https://doi.org/10.1137/20M1373384
}
}
33. Reduced model-based parareal simulations of oscillatory singularly perturbed ordinary differential equations
L. Grigori, S. A. Hirstoaga, V-T. Nguyen and J. Salomon
Journal of Computational Physics (2021)
@article{GRIGORI2021110282,
title = {Reduced model-based parareal simulations of oscillatory singularly perturbed ordinary differential equations},
journal = {Journal of Computational Physics},
volume = {436},
pages = {110282},
year = {2021},
issn = {0021-9991},
doi = {https://doi.org/10.1016/j.jcp.2021.110282},
url = {https://www.sciencedirect.com/science/article/pii/S0021999121001777},
author = {Laura Grigori and Sever A. Hirstoaga and Van-Thanh Nguyen and Julien Salomon},
keywords = {Parareal algorithm, Two-scale expansion, Multi-scale models, Vlasov characteristics, Electric and magnetic fields},
abstract = {We propose a new strategy for solving by the parareal algorithm highly oscillatory ordinary differential equations which are characteristics of a six-dimensional Vlasov equation. For the coarse solvers we use reduced models, obtained from the two-scale asymptotic expansions in [4]. Such reduced models have a low computational cost since they are free of high oscillations. The parareal method allows to improve their accuracy in a few iterations through corrections by fine solvers of the full model. We demonstrate the accuracy and the efficiency of the strategy in numerical experiments of short time and long time simulations of charged particles submitted to a large magnetic field. In addition, the convergence of the parareal method is obtained uniformly with respect to the vanishing stiff parameter.}
}
34. Greedy reconstruction algorithm for the identification of spin distribution
S. Buchwald, G. Ciaramella , J. Salomon and D. Sugny
Physical Review A (2021)
@article{PhysRevA.104.063112,
title = {Greedy reconstruction algorithm for the identification of spin distribution},
author = {Buchwald, S. and Ciaramella, G. and Salomon, J. and Sugny, D.},
journal = {Phys. Rev. A},
volume = {104},
issue = {6},
pages = {063112},
numpages = {9},
year = {2021},
month = {Dec},
publisher = {American Physical Society},
doi = {10.1103/PhysRevA.104.063112},
url = {https://link.aps.org/doi/10.1103/PhysRevA.104.063112}
}
35. Optimal periodic resource allocation in reactive dynamical systems: Application to microalgal production
O. Bernard, L. Lu, J Salomon
Int. J. Robust and Nonlinear Control (2023)
@article{https://doi.org/10.1002/rnc.6171,
author = {Bernard, Olivier and Lu, Liu-Di and Salomon, Julien},
title = {Optimal periodic resource allocation in reactive dynamical systems: Application to microalgal production},
journal = {International Journal of Robust and Nonlinear Control},
volume = {33},
number = {9},
pages = {4989-5010},
keywords = {assignment problem, dynamical system, impulse control, linear approximation, microalgae production, nonlinear problems, periodic control, periodic system, permutation, resource allocation, switched systems},
doi = {https://doi.org/10.1002/rnc.6171},
url = {https://onlinelibrary.wiley.com/doi/abs/10.1002/rnc.6171},
eprint = {https://onlinelibrary.wiley.com/doi/pdf/10.1002/rnc.6171},
abstract = {Abstract In this article, we focus on a periodic resource allocation problem applied on a dynamical system which comes from a biological system. More precisely, we consider a system with N\$\$ N \$\$ resources and N\$\$ N \$\$ activities, each activity use the allocated resource to evolve up to a given time T>0\$\$ T>0 \$\$ where a control (represented by a given permutation) will be applied on the system to reallocate the resources. The goal is to find the optimal control strategies which optimize the cost or the benefit of the system. This problem can be illustrated by an industrial biological application, namely, the optimization of a mixing strategy to enhance the growth rate in a microalgal raceway system. A mixing device, such as a paddle wheel, is considered to control the rearrangement of the depth of the algae cultures, hence the light perceived at each lap. We prove that if the dynamics of the system is periodic, then the period corresponds to one reallocation whatever the order of the involved permutation matrix is. A nonlinear optimization problem for one reallocation process is then introduced. Since N!\$\$ N! \$\$ permutations need to be tested in the general case, it can be numerically solved only for a limited number of N\$\$ N \$\$. To overcome this difficulty, we introduce a second optimization problem which provides a suboptimal solution of the initial problem, but whose solution can be determined explicitly. A sufficient condition to characterize cases where the two problems have the same solution is given. Some numerical experiments are performed to assess the benefit of optimal strategies in various settings.},
year = {2023}
}
}
36. A parareal algorithm for a highly oscillating Vlasov-Poisson system with
reduced models for the coarse solving
L. Grigori, S. Hirstoaga, J. Salomon
Computers & Mathematics with Applications (2023)
@article{ WOS:000911730200001,
Author = {Grigori, Laura and Hirstoaga, Sever A. and Salomon, Julien},
Title = {A parareal algorithm for a highly oscillating Vlasov-Poisson system with
reduced models for the coarse solving},
Journal = {COMPUTERS \& MATHEMATICS WITH APPLICATIONS},
Year = {2023},
Volume = {130},
Pages = {137-148},
Month = {JAN 15},
Abstract = {In this paper, we introduce a new strategy for solving highly
oscillatory two-dimensional Vlasov-Poisson systems by means of a
specific version of the parareal algorithm. The novelty consists in
using reduced models, obtained from the two-scale convergence theory,
for the coarse solving. The reduced models are useful to approximate the
original Vlasov-Poisson model at a low computational cost since they are
free of high oscillations. Both models are numerically solved in a
particle-in-cell framework. We illustrate this strategy with numerical
experiments based on long time simulations of a charged beam in a
focusing channel and under the influence of a rapidly oscillating
external electric field. On the basis of computing times, we provide an
analysis of the efficiency of the parareal algorithm in terms of
speedup.},
DOI = {10.1016/j.camwa.2022.12.004},
EarlyAccessDate = {DEC 2022},
ISSN = {0898-1221},
EISSN = {1873-7668},
Unique-ID = {WOS:000911730200001},
}
37. Discrete entropy inequalities via an optimization process
N. Aguillon, E. Audusse, V. Desveaux, J. Salomon
M2AN (2024)
@article{ WOS:001176756900002,
Author = {Aguillon, Nina and Audusse, Emmanuel and Desveaux, Vivien and Salomon,
Julien},
Title = {DISCRETE ENTROPY INEQUALITIES VIA AN OPTIMIZATION PROCESS},
Journal = {ESAIM-MATHEMATICAL MODELLING AND NUMERICAL ANALYSIS},
Year = {2024},
Volume = {58},
Number = {1},
Pages = {363-391},
Month = {FEB 28},
Abstract = {The solutions of hyperbolic systems may contain discontinuities. These
weak solutions verify not only the original PDEs, but also an entropy
inequality that acts as a selection criterion determining whether a
discontinuity is physical or not. Obtaining a discrete version of these
entropy inequalities when approximating the solutions numerically is
crucial to avoid convergence to unphysical solutions or even
unstability. However such a task is difficult in general, if not
impossible for schemes of order 2 or more. In this paper, we introduce
an optimization framework that enables us to quantify a posteriori the
decrease or increase of entropy of a given scheme, locally in space and
time. We use it to obtain maps of numerical diffusion and to prove that
some schemes do not have a discrete entropy inequality. A special
attention is devoted to the widely used second order MUSCL scheme for
which almost no theoretical results are known.},
DOI = {10.1051/m2an/2023098},
ISSN = {2822-7840},
EISSN = {2804-7214},
Unique-ID = {WOS:001176756900002},
}
38. A SPIRED code for the reconstruction of spin distribution
S. Buchwald, G. Ciaramella, J. Salomon, D. Sugny
Computer Physics Communications (2024)
@article{ WOS:001187851900001,
Author = {Buchwald, Simon and Ciaramella, Gabriele and Salomon, Julien and Sugny,
Dominique},
Title = {A SPIRED code for the reconstruction of spin distribution},
Journal = {COMPUTER PHYSICS COMMUNICATIONS},
Year = {2024},
Volume = {299},
Month = {JUN},
Abstract = {In Nuclear Magnetic Resonance (NMR), it is of crucial importance to have
an accurate knowledge of the spin probability distribution corresponding
to inhomogeneities of the magnetic fields. An accurate identification of
the sample distribution requires a set of experimental data that is
sufficiently rich to extract all fundamental information. These data
depend strongly on the control fields (and their number) used
experimentally to perturb the spin system. In this work, we present and
analyze a greedy reconstruction algorithm, and provide the corresponding
SPIRED code, for the computation of a set of control functions allowing
the generation of data that are appropriate for the accurate
reconstruction of a sample probability distribution. In particular, the
focus is on NMR and spin dynamics governed by the Bloch system with
inhomogeneities in both the static and radio -frequency magnetic fields
applied to the sample. We show numerically that the algorithm is able to
reconstruct non trivial joint probability distributions of the two
inhomogeneous Hamiltonian parameters. A rigorous convergence analysis of
the algorithm is also provided.},
DOI = {10.1016/j.cpc.2024.109126},
EarlyAccessDate = {FEB 2024},
Article-Number = {109126},
ISSN = {0010-4655},
EISSN = {1879-2944},
ORCID-Numbers = {Buchwald, Simon/0009-0004-2350-4399},
Unique-ID = {WOS:001187851900001},
}
39. Acceleration of a wave-structure interaction solver by the Parareal
method
Y. Poirier, J. Salomon, A. Babarit, P. Ferrant, G. Ducrozet
Engineering Analysis with Boundary Elements (2024)
@article{ WOS:001270631600001,
Author = {Poirier, Yohan and Salomon, Julien and Babarit, Aurelien and Ferrant,
Pierre and Ducrozet, Guillaume},
Title = {Acceleration of a wave-structure interaction solver by the Parareal
method},
Journal = {ENGINEERING ANALYSIS WITH BOUNDARY ELEMENTS},
Year = {2024},
Volume = {167},
Month = {OCT},
Abstract = {Potential flow theory-based solvers are commonly used in ocean
engineering to investigate the interactions between ocean waves and
floating bodies. Depending on assumptions, several methods have been
proposed. Among them, the Weak-Scatterer method is an interesting
trade-off in the sense that this approach is not limited in theory by
the small wave amplitudes and small body motions assumptions of linear
methods. Moreover, this approach is in practice more stable than the
fully non-linear methods. An implementation of the Weak-Scatterer method
is the WS-CN code (Letournel, 2015; Chauvign \& eacute;, 2016;
Wuillaume, 2019). The computational time of the WS-CN code which is
considered in the present study is relatively long for engineering
purposes. In order to reduce it, the present paper presents an
implementation of the Parareal method in the WS-CN code. The Parareal
method is an algorithm for parallelizing a simulation in time that can
accelerate the complete simulation (Lions, 2001) . This is a key
difference in comparison to other acceleration techniques which have
been studied in the literature (e.g. the Fast Multipole Method (FMM),
the precorrected Fast Fourier Transform (pFFT) method, ... ). To the
authors' knowledge, the present study is the first to couple the
Parareal method to a potential flow theory-based wave-structure
interaction solver. It is shown that the method can significantly reduce
the computational time for small wave steepness, but that the
performance decreases rapidly with increasing steepness.},
DOI = {10.1016/j.enganabound.2024.105870},
EarlyAccessDate = {JUL 2024},
Article-Number = {105870},
ISSN = {0955-7997},
EISSN = {1873-197X},
ResearcherID-Numbers = {Ducrozet, Guillaume/F-5761-2012
},
ORCID-Numbers = {Babarit, Aurelien/0000-0002-6329-9711},
Unique-ID = {WOS:001270631600001},
}