

Ce travail porte sur la décomposition de mouvement dans le cadre de la dynamique des milieux continus. Dans ce domaine, la plupart des modèles sont non-linéaires et nécessitent des sous-boucles de résolution coûteuses, en particulier lorsque les mouvements sont rapides par rapport aux déformations élastiques. Précisément, le calcul d’une déformation élastique d est alors très difficile à évaluer d’un pas de temps à l’autre : les techniques de linéarisation détériorent l’approximation et sans linéarisation, les sous-boucles convergent difficilement. Face à ce problème, les ingénieurs factorisent le mouvement en une partie solide et une partie purement élastique u, ne comportant ni translation, ni rotation globale. La figure résume cette méthode. L’énergie élastique E vérifie alors E(d) = E(u) et u est de norme plus petite que d donc plus facile à traiter. Le problème est que cette formulation, dite corotationnelle, est généralement associée à des discrétisations ne préservant numériquement ni l’énergie mécanique, ni le moment cinétique.
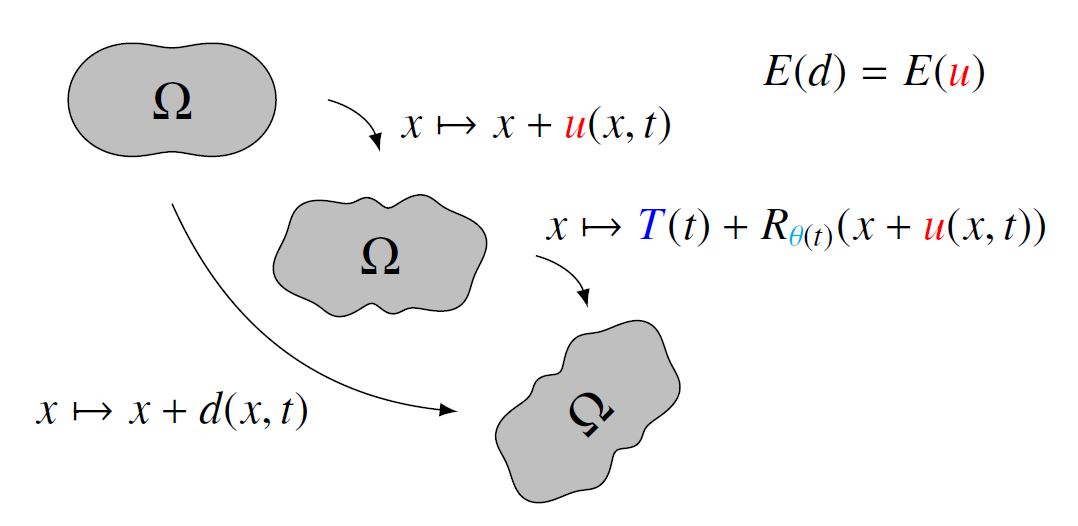
Cet état de fait nous a conduit à proposer un schéma numérique conservatif en adaptant certaines idées du schéma de Crank-Nicholson au mouvement relatif exprimé dans le référentiel du mouvement solide. La caractérisation du terme de rotation dans ce dernier s’avéra délicate : les non-linéarités engendrées par le changement de référentiel s’ajoutent à celles du terme élastique pour rendre en effet un découplage des variables compliqué.
Nous avons surmonté ce problème par l’introduction d’une variable auxiliaire, la vitesse relative et une condition d’orthogonalité entre le mouvement solide et la déformation élastique. On a ensuite montré l’existence de solutions au système discrétisé et obtenu des bornes pour en faciliter la résolution. Numériquement, l’algorithme permet une linéarisation efficace pour les petites déformations et réduit les sous-itérations dans le cas non-linéaire.
La dernière partie de la contribution se concentre sur la dimension trois où la rotation est vectorielle. Dans un second travail, nous a rejoint, nous avons couplé l’algorithme avec des méthodes de traitement du contact. Ce travail technique a ainsi donné lieu à une adaptation des algorithmes de Laursen et Chawla pour la friction et de la primal-dual active set strategy de Kunisch et Ito, pour la détermination des points de contact. Malgré trois sous-boucles internes (concernant l’angle de rotation, le contact et le frottement), les résultats sur des benchmarks ont été reproduits avec un faible coût de calcul.
À ma connaissance, il n’existait pas de discrétisation spécifique à la formulation corotationnelle avant notre travail. La difficulté fut ici d’ordre algébrique : trouver une discrétisation qui assure le bilan d’énergie à chaque pas de temps a nécessité de nombreuses tentatives.
Les publications liées à cette contribution sont [6] et [8].