

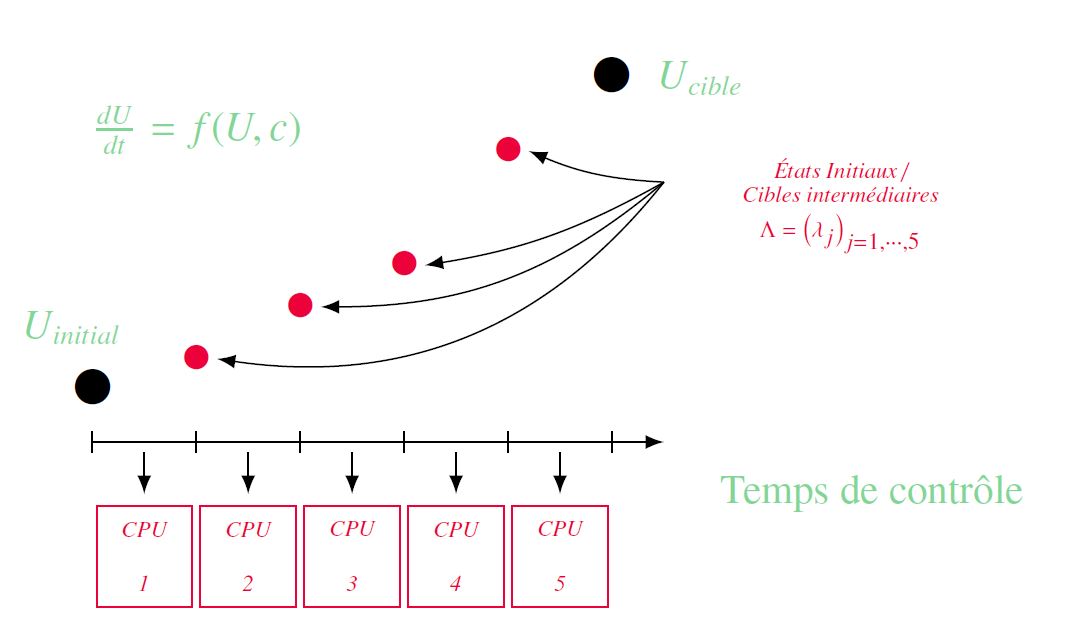
Dans cette contribution, nous avons construit une nouvelle méthode de parallélisation en temps dédiée à la résolution de systèmes d’optimalité issus de problèmes de contrôle. Le but est d’approcher en un temps T un état cible en partant d’une condition initiale fixée. Pour paralléliser la résolution, notre approche consiste à fixer des états intermédiaires, jouant tantôt le rôle de condition initiale tantôt celui de cible selon le sous-intervalle de la décomposition considéré. Des contrôles optimaux partiels peuvent alors être calculés en parallèle puis concaténés pour permettre une mise à jour des états intermédiaires. L’algorithme exploite l’idée de poursuite de trajectoire : les états intermédiaires sont construits par interpolation de la trajectoire directe et d’une trajectoire de référence, donnée par l’adjoint, menant à l’état cible au temps T. La figure donne une représentation schématique de cette stratégie. Cette approche intuitive a ensuite été complétée par une formalisation qui permet d’identifier l’algorithme à une méthode de direction alternée. Dans ce cadre, on a prouvé la convergence de l’approximation vers la solution obtenue sans parallélisation.
D’un point de vue pratique, le temps de résolution a été approximativement divisé par 8 en utilisant 10 sous-intervalles, ce qui est proche de l’efficacité totale, c’est-à-dire du cas où le temps de calcul est divisé par le nombre de processeurs.
Ce travail correspond à la publication [4]. La méthode qui vient d’être décrite s’applique à des équations hyperboliques pour lesquelles l’état adjoint suit une dynamique de même nature que l’état à contrôler : les états intermédiaires sont calculés par interpolation de trajectoires directes et adjointes.
La thèse de Kamel Riahi nous a permis d’étendre la notion de points intermédiaires au cas parabolique, où les trajectoires sont irréversibles.
La méthode proposée repose sur la construction d’une trajectoire de référence, cette fois-ci distincte de la trajectoire adjointe du problème de contrôle.
La convergence a également été obtenue théoriquement [Note 4].
Nous travaillons actuellement sur l’obtention de l’efficacité totale. Un article sera bientôt soumis [Preprint 1].
La démarche générale consistant à définir des états intermédiaires se retrouve dans les méthodes dites "multishooting".
Les états intermédiaires y sont cependant définis uniquement à partir de questions de continuité, et non d’optimalité. De plus ces algorithmes reposent sur une méthode de résolution des sous-problèmes particulière : la méthode de tir, elle-même basée sur des itérations de Newton. Notre approche a une portée plus générale, puisqu’elle part d’une méthode générique de résolution des sous-problèmes, qu’elle utilise en "boîte noire".
Les publications liées à cette contribution sont [4], [Note 4] et [Preprint 1].