De même que pour la parallélisation, il est aussi question d’accélération de calcul dans ce travail. L’idée est ici de profiter d’une phase préliminaire de calcul dite hors-ligne pour rendre les simulations plus rapides, par exemple en réduisant le nombre de variables. Cette approche est utilisée dans la méthode de base réduite. Dans cette méthode dédiée aux problèmes paramétrés, on précalcule finement un certain nombre de solutions numériques – les échantillons – d’une équation en faisant varier ses paramètres. On extrait alors de cet ensemble une famille de petite taille qui est ensuite utilisée comme base de Galerkin pour calculer une solution dite réduite dans la phase en ligne. L’enjeu est de construire ces familles de sorte qu’elles approchent bien l’ensemble des solutions fines. Une approche dite "gloutonne" apparue dans les années 2000 consiste à utiliser un estimateur d’erreur entre les solutions fine et réduite : la base est construite en incluant itérativement la solution fine correspondant au jeu de paramètre produisant la plus grande estimation d’erreur.
Ces questions ont connu ces dernières années beaucoup de développements, mais ne couvraient pas de problèmes liés à des inégalités variationnelles. Pour réaliser cette extension [18], nous avons introduit un cadre fonctionnel adapté et analysé la méthode en obtenant un estimateur a posteriori de l’erreur. La dénomination "a posteriori" signifie que l’erreur est estimée seulement à partir de la solution réduite et est donc peu coûteuse en calcul. Notre approche est basée sur l’introduction de résidus spécifiques au système de Karush-Kuhn-Tucker à résoudre. Dans un second travail [23], la méthode est étendue aux équations d’évolution, avec pour application le calcul du prix d’une option américaine, dans un modèle de Balck et Scholes. La difficulté fut d’étendre l’analyse d’erreur à des schémas itératifs en temps. Nous avons obtenu un estimateur basé sur une norme de type énergie couvrant l’ensemble de la trajectoire.
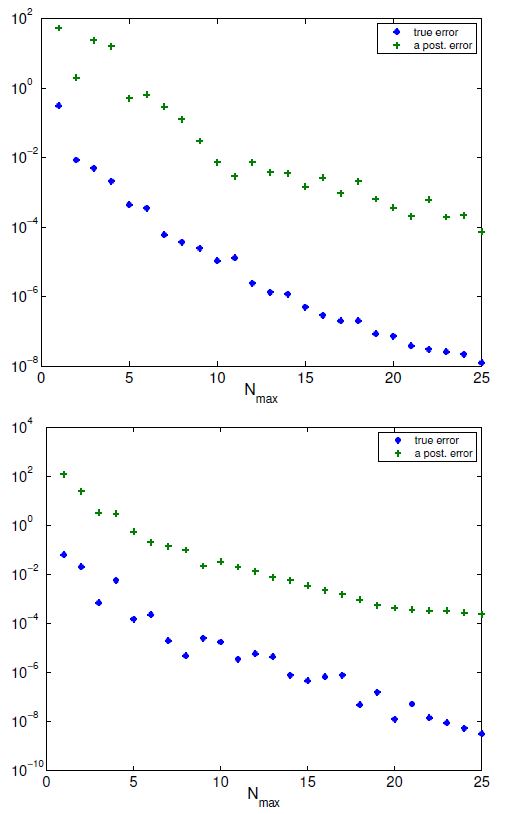
Les figures montrent la décroissance de l’erreur et de l’estimateur lors de la construction gloutonne. Les estimateurs utilisés sont la vraie erreur (en haut), et l’estimateur a posteriori (en bas), d’où les allures monotones des suites. Beaucoup moins coûteux, ce dernier donne de résultats analogues (et même meilleurs dans cet exemple).
La construction de l’estimateur d’erreur a été la difficulté levée par ce travail. Il a fallu adapter la notion de résidu
au cas d’inégalités, ce que nous avons fait en introduisant un projecteur, qui, bien qu’agissant sur des vecteurs de grandes dimensions, reste facile à calculer puisqu’il consiste simplement à retirer les composantes positives.
Les publications liées à cette contribution sont [18], [23] et [Note 3].