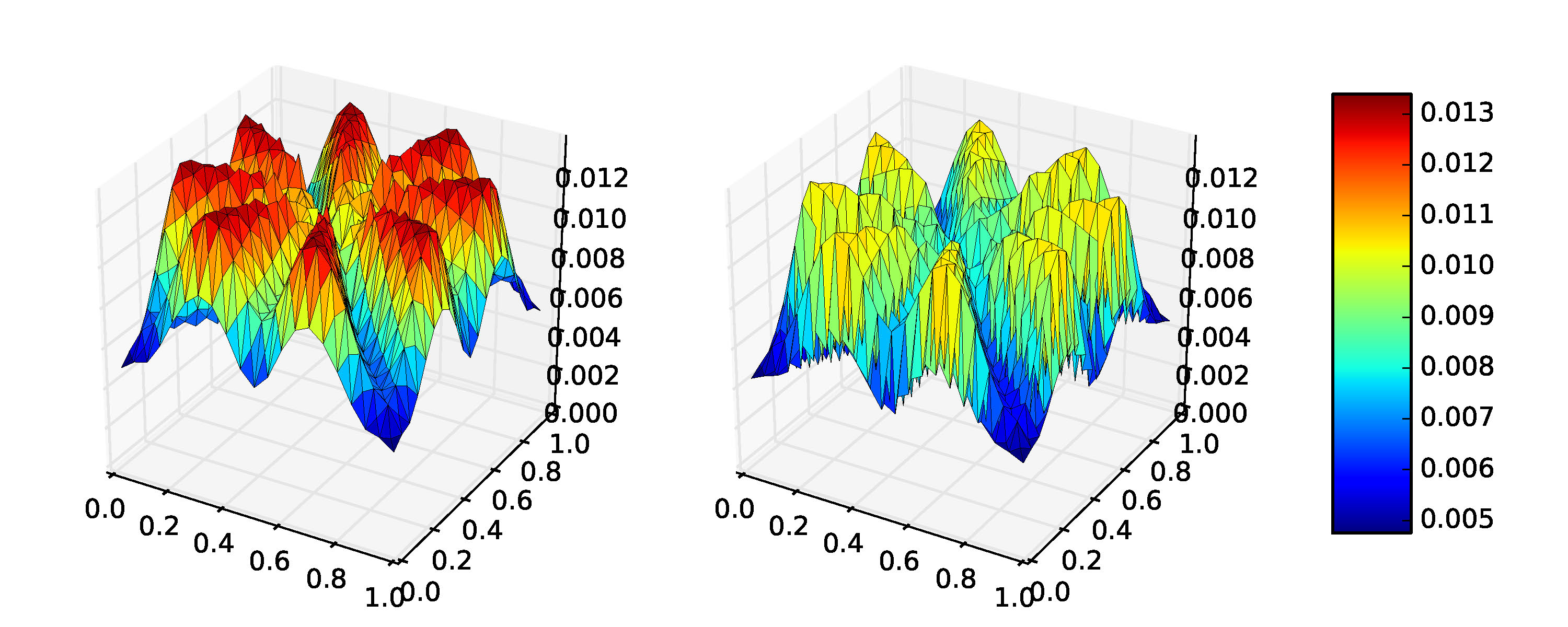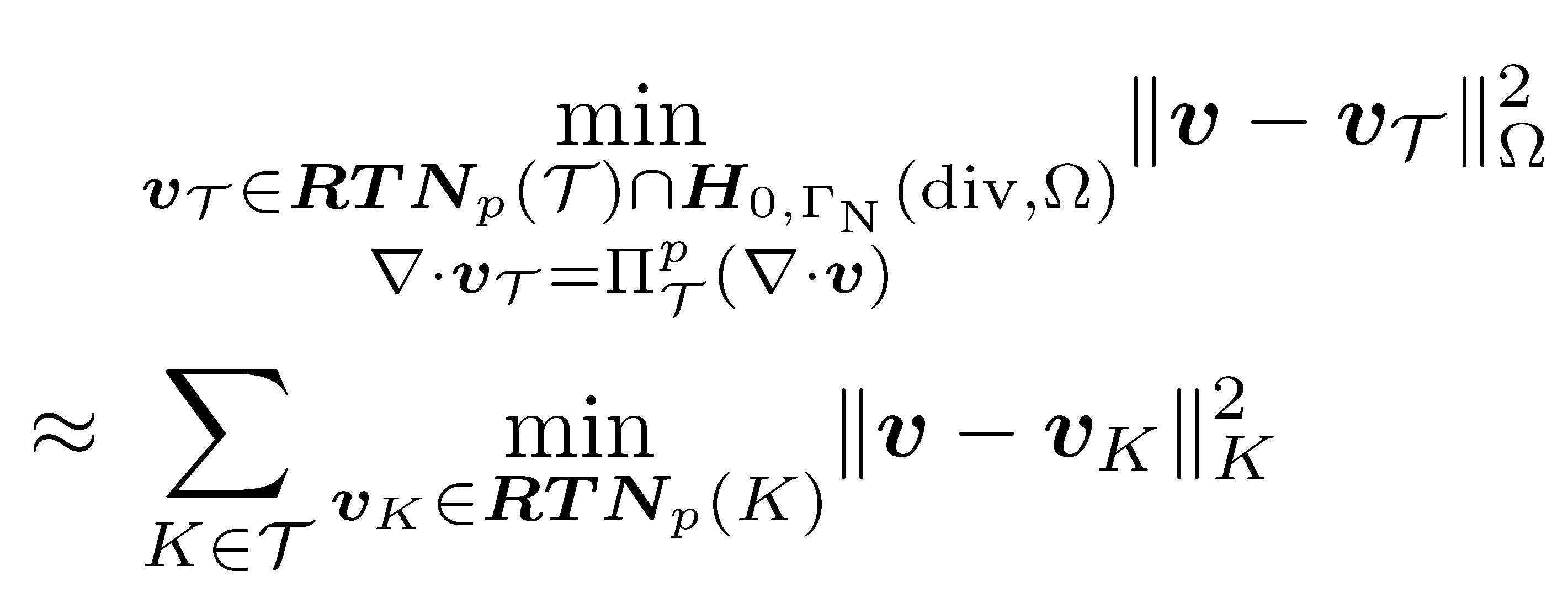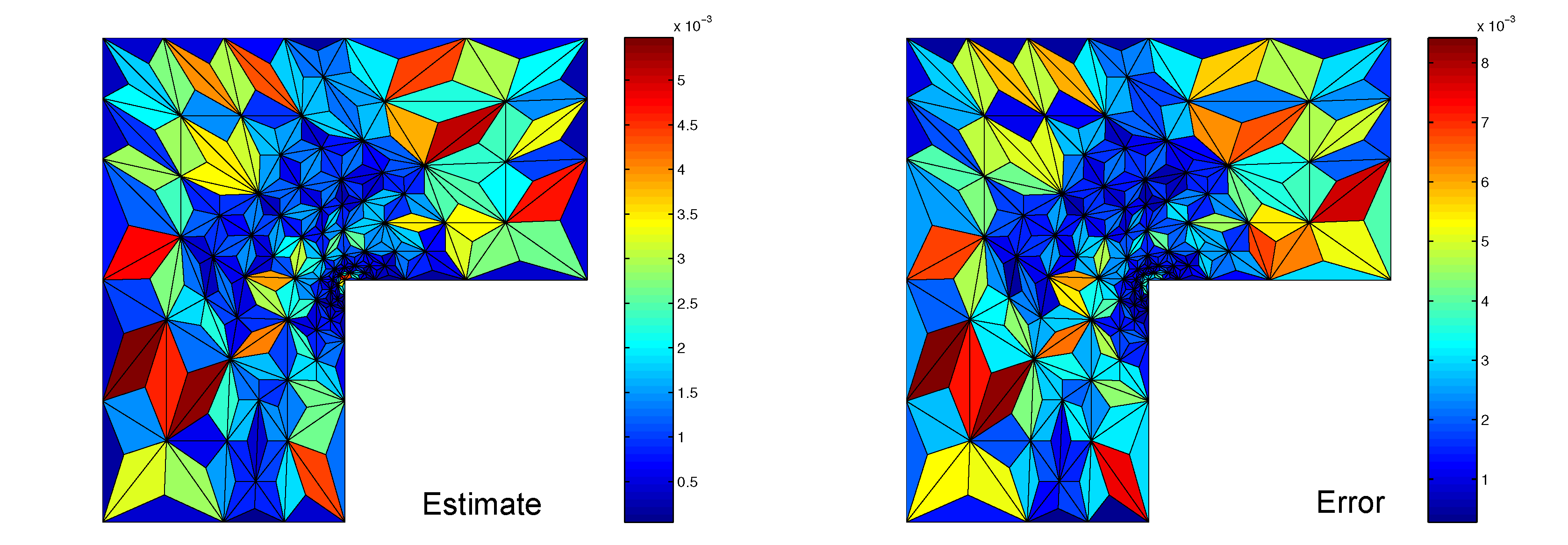
Estimations d'erreur a posteriori A posteriorní odhady chyb A posteriori error estimatesPermettent d'estimer la taille et la distribution d'erreur dans les simulations numériques. Umožňují odhadnout velikost a rozložení chyby v numerických simulacích. Enable to predict the size and distribution of the error in numerical simulations. |
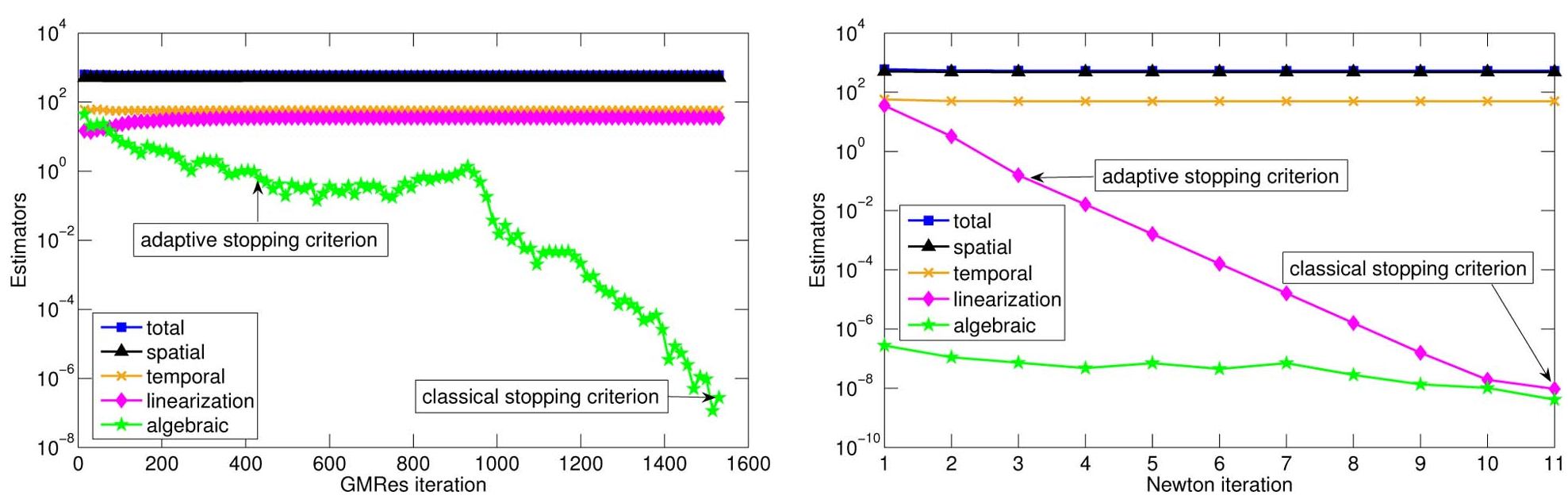
Critères d'arrêt pour pour des solveurs itératifs Zastavovací kritéria pro iterační řešiče Stopping criteria for iterative solversPermettent de comparer la taille de différentes composantes d'erreur, toutes en unités physiques des flux. Umožňují porovnat velikost různých složek chyby, vždy ve fyzikálních jednotkách toků. Enable to compare the size of the different error components, all in flux physical units. |
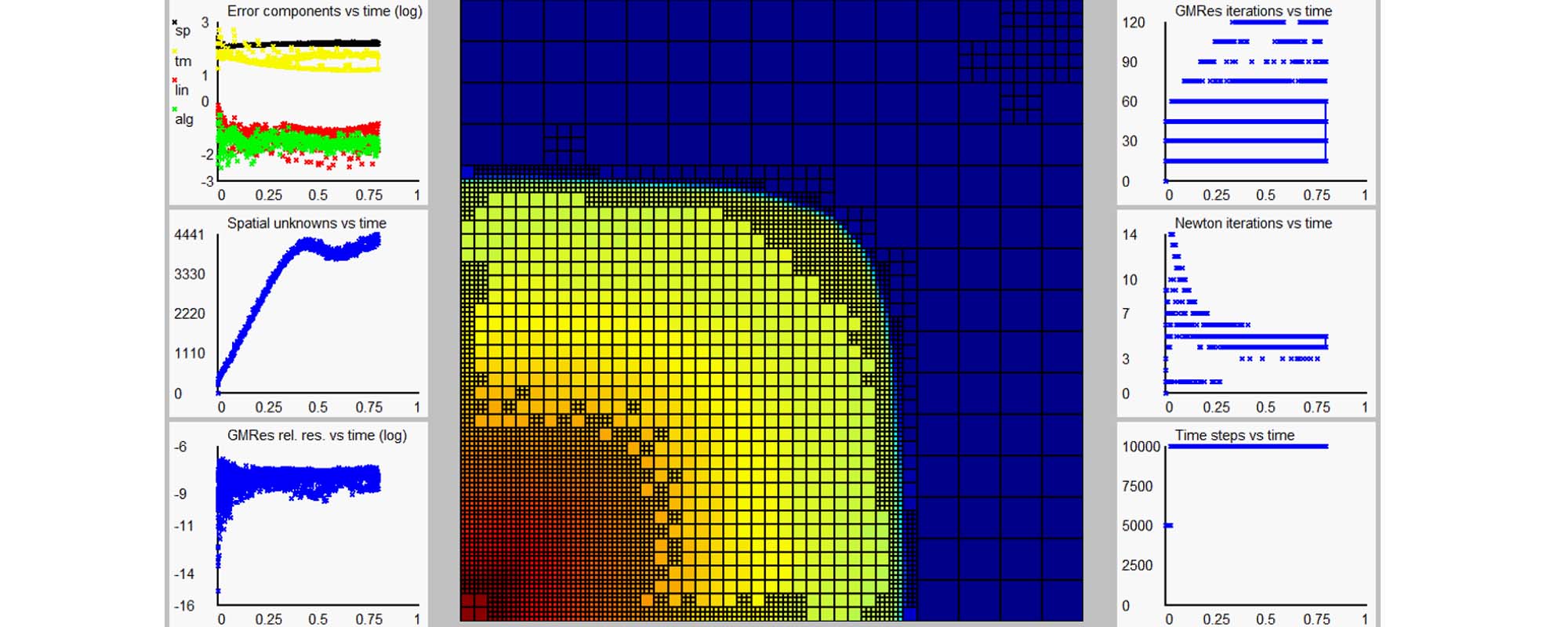
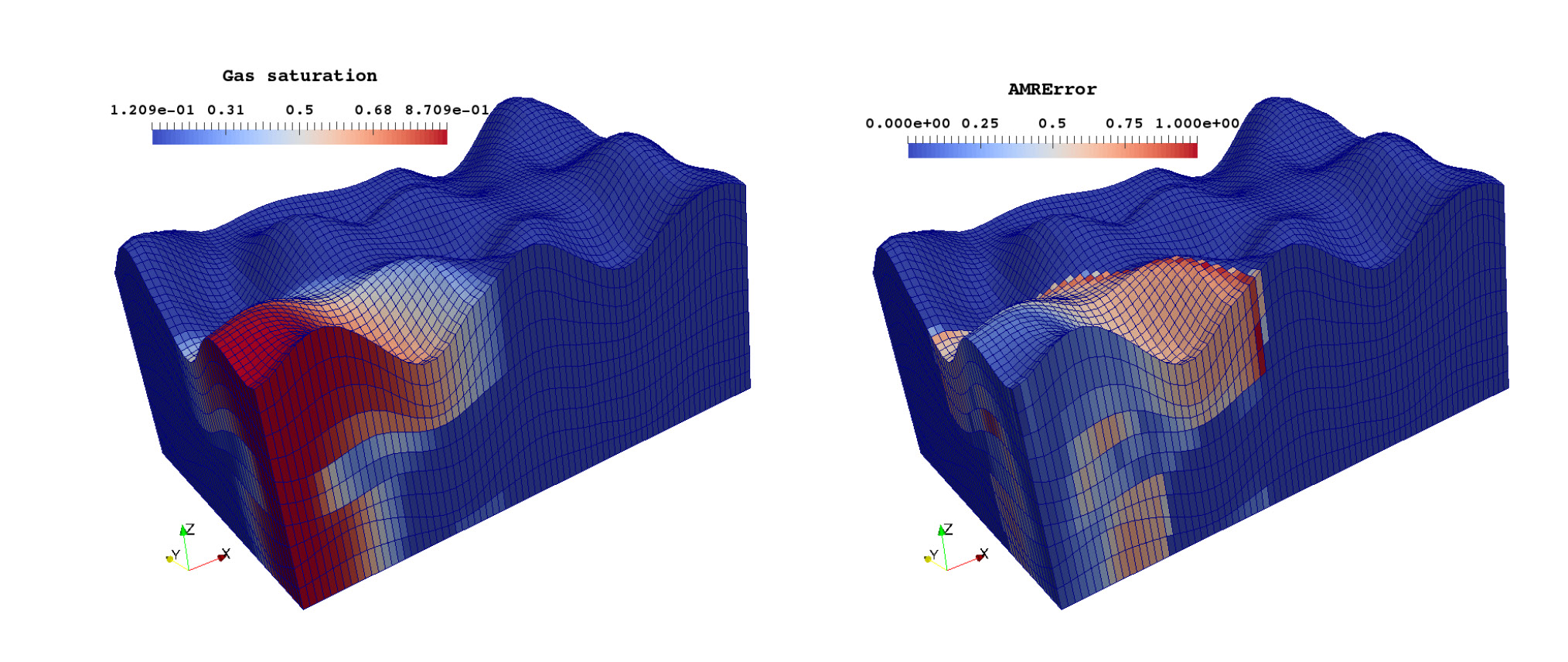
Adaptivité et applications au milieu poreux Adaptivita a aplikace v porézním prostředí Adaptivity and applications to porous mediaAdaptivité combinée du solveur et du maillage et applications aux écoulements en milieu poreux. Kombinovaná adaptivita řešiče a sítě a aplikace na proudění v porézním prostředí. Combined solver and mesh adaptivity and applications to simulation of porous media flows. |
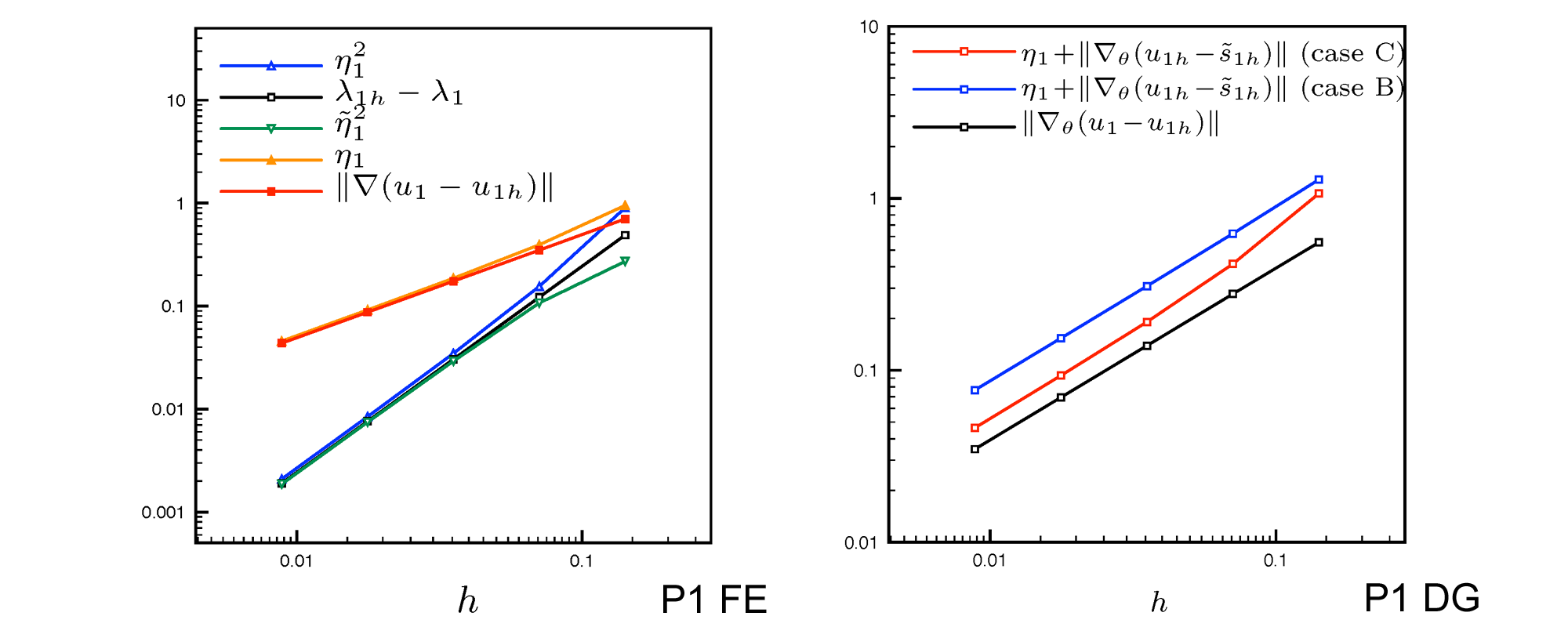
Raffinement hp et robustesse au degré polynomial hp zjemňování a robustnost vůči polynomiálnímu stupni hp-refinement and polynomial-degree-robustnessConvergence exponentielle par rapport au nombre de degrés de liberté et optimalité théorique. Exponenciální konvergence vzhledem k počtu stupňů volnosti a teoretická optimalita. Exponential convergence with respect to the number of degrees of freedom and theoretical optimality. |
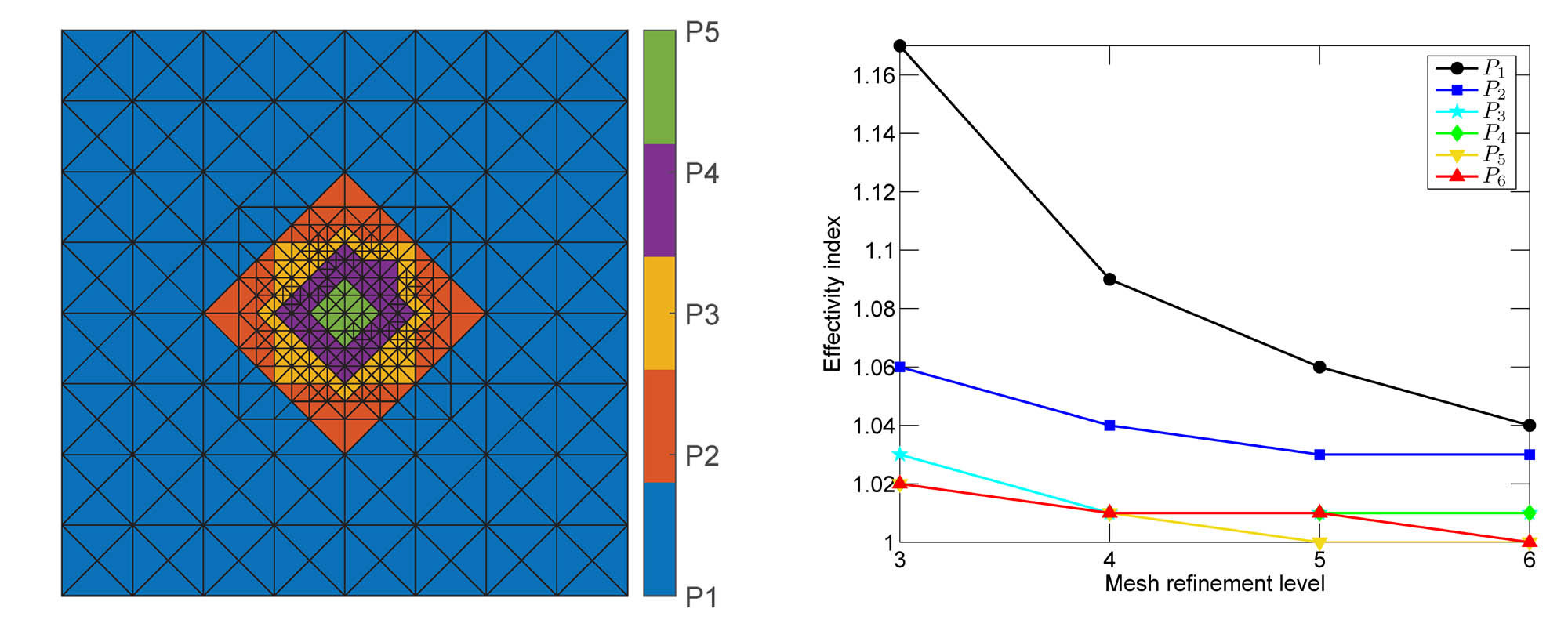
Bornes garanties pour les valeurs et vecteurs propres Zaručné odhady pro vlastní čísla a vektory Guaranteed bounds for eigenvalues and eigenvectorsSimples, multiples ou clusters. Jednoduchá, násobná i klustry. Simple, multiple, or a cluster. |