Patrik DANIEL

Research interests

Finite elements ◼ Adaptivity (in its many forms) ◼ A posteriori error estimation ◼ High Performance Computing ◼ Programming

We proposed a new practical adaptive refinement strategy for hp-finite element approximations of elliptic problems. Following recent theoretical developments in polynomial-degree-robust a posteriori error analysis, we solve two types of discrete local problems on vertex-based patches. The first type involves the solution on each patch of a mixed finite element problem with homogeneous Neumann boundary conditions, which leads to an H(div,Ω)-conforming equilibrated flux. This, in turn, yields a guaranteed upper bound on the error and serves to mark mesh vertices for refinement via Dörfler's bulk-chasing criterion. The second type of local problems involves the solution, on patches associated with marked vertices only, of two separate primal finite element problems with homogeneous Dirichlet boundary conditions, which serve to decide between h-, p- or hp-refinement. Altogether, we show that these ingredients lead to a computable guaranteed bound on the ratio of the errors between successive refinements (error reduction factor).

HAL

arXiv

The results obtained with the smooth test case:

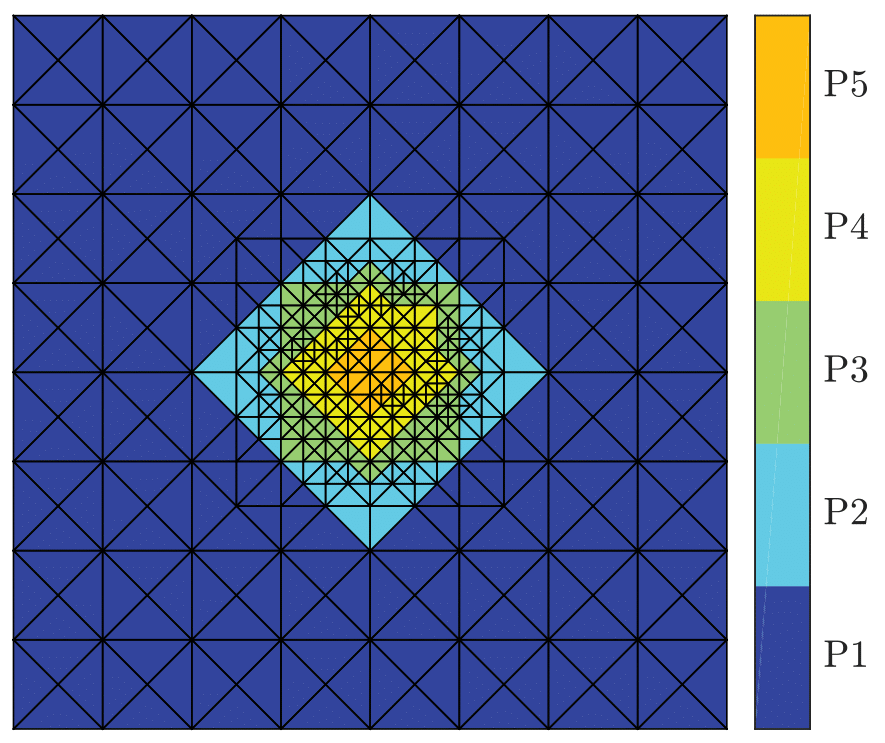
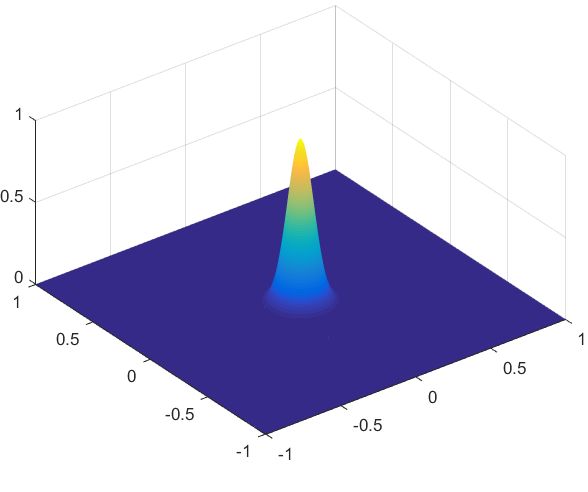
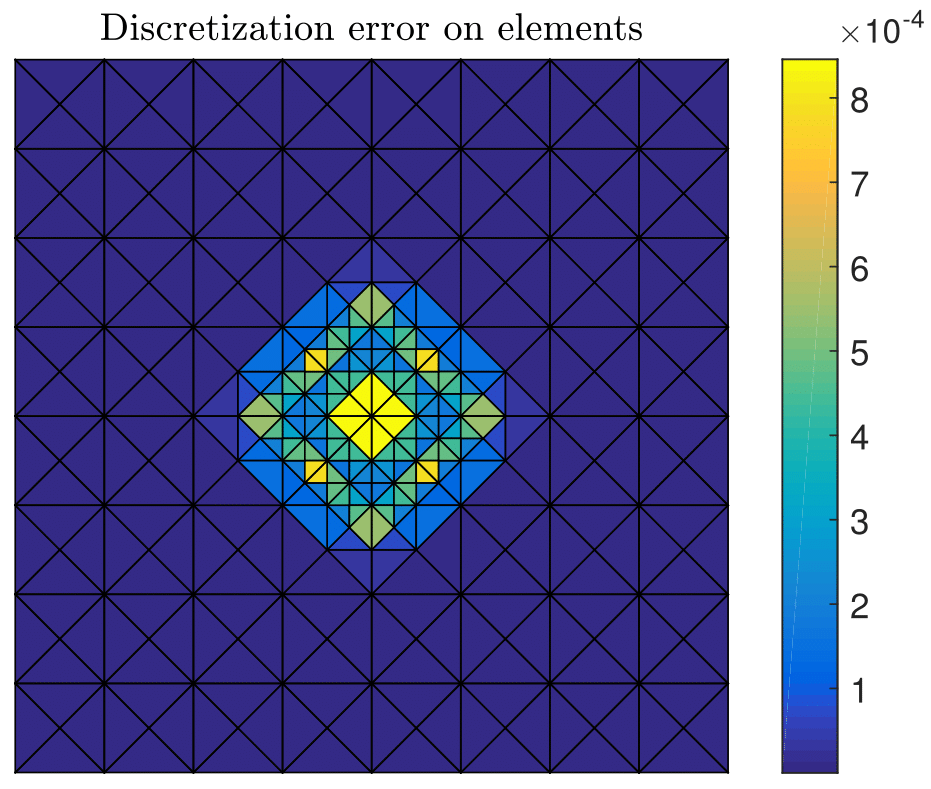
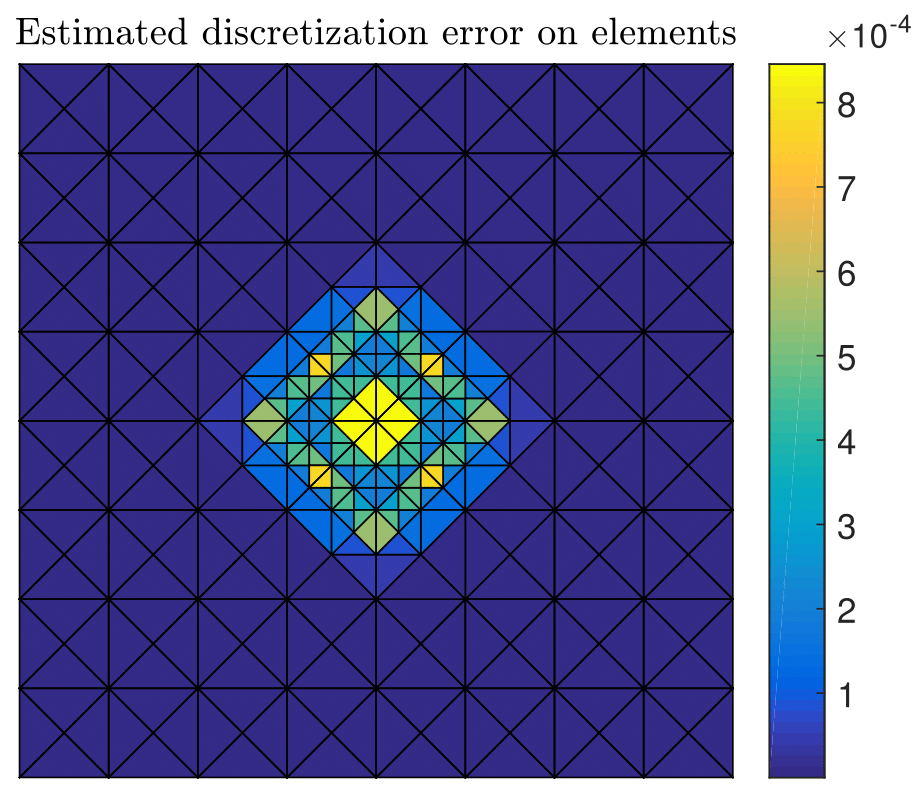
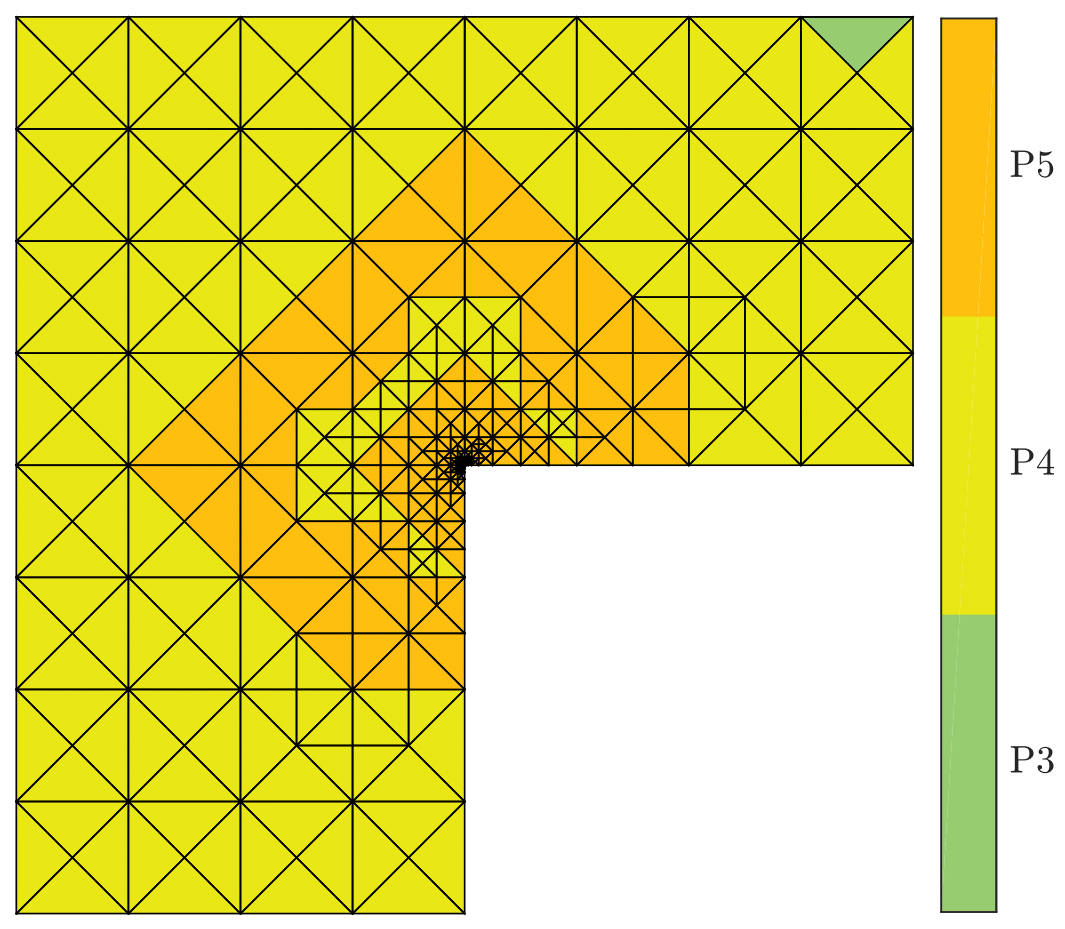
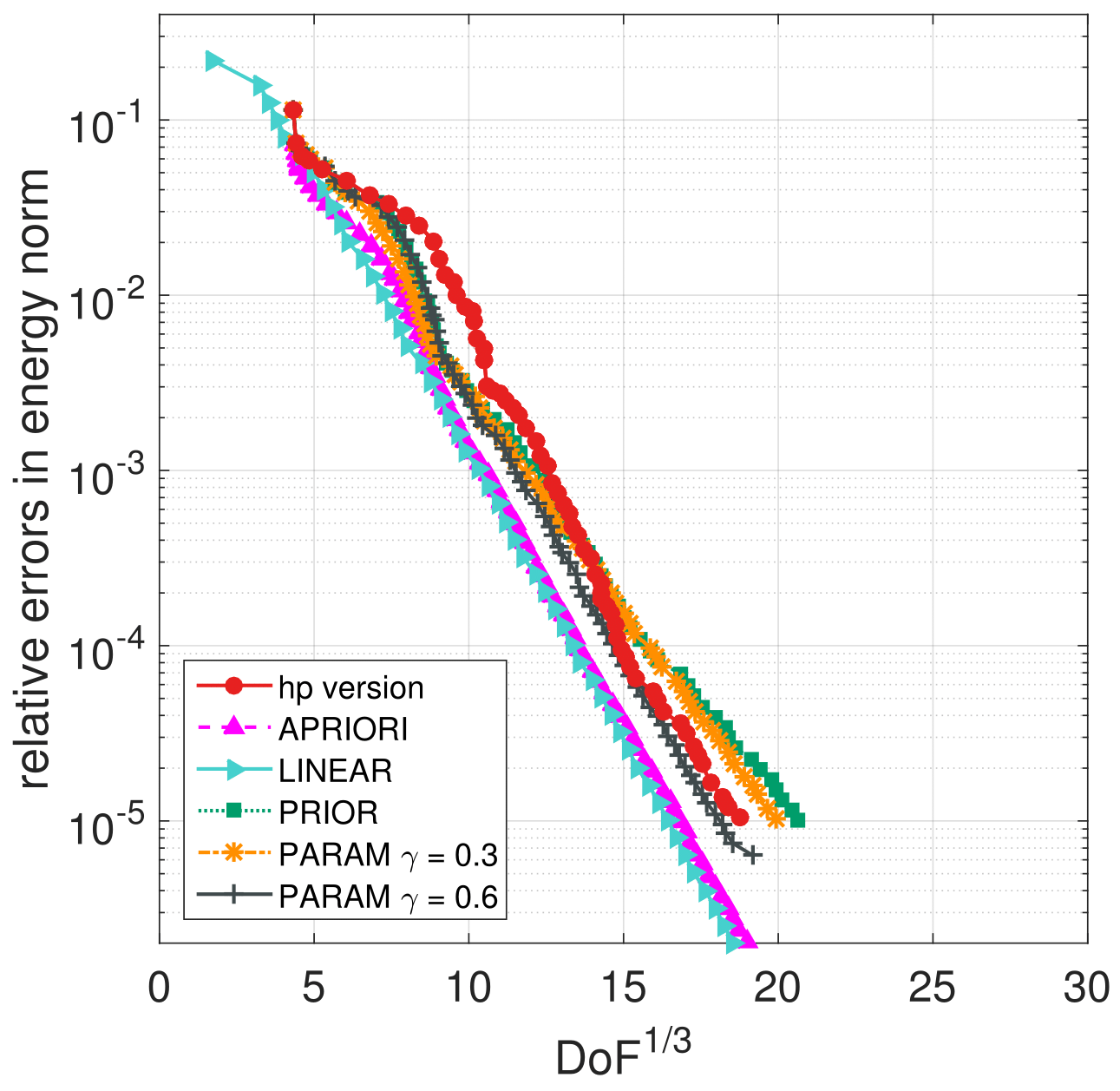
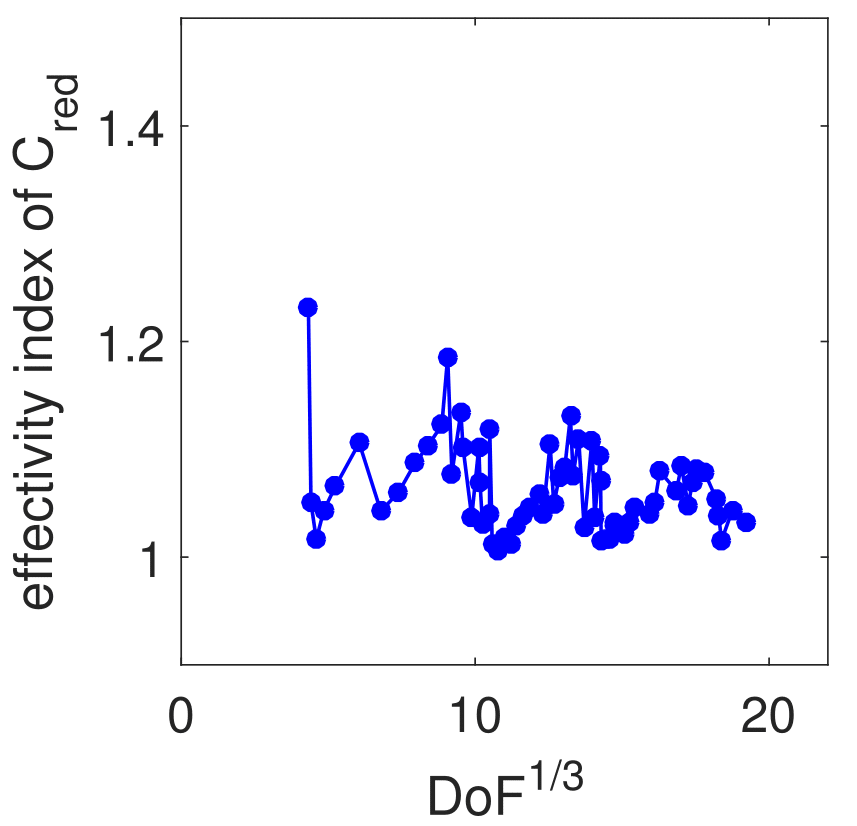
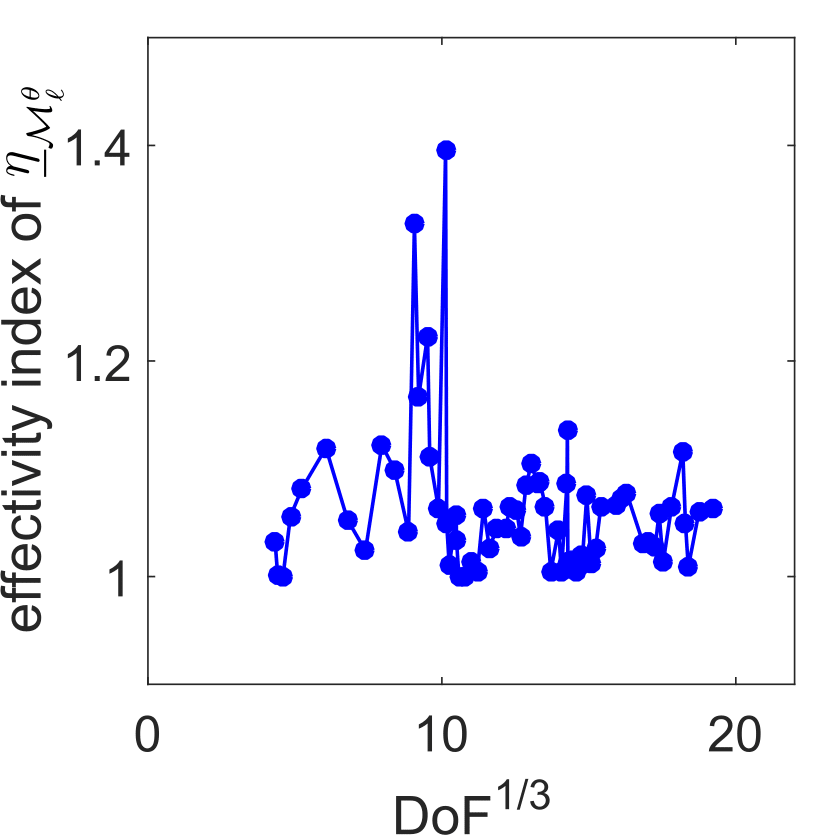
The results obtained with the test case with singular exact solution:

This work was also extended by taking into account an inexact algebraic solver. Namely, on each level of refinement and on each iteration of an (arbitrary) iterative algebraic solver, we compute guaranteed a posteriori error bounds on the algebraic and the total errors in energy norm. For the algebraic error upper bound, we crucially exploit the nested hierarchy of $hp$-finite element spaces created throughout the adaptive algorithm, whereas the total error bound is computed using the finest space only. These error bounds allow us to formulate adaptive stopping criteria for the algebraic solver ensuring that the algebraic error does not significantly contribute to the total error.

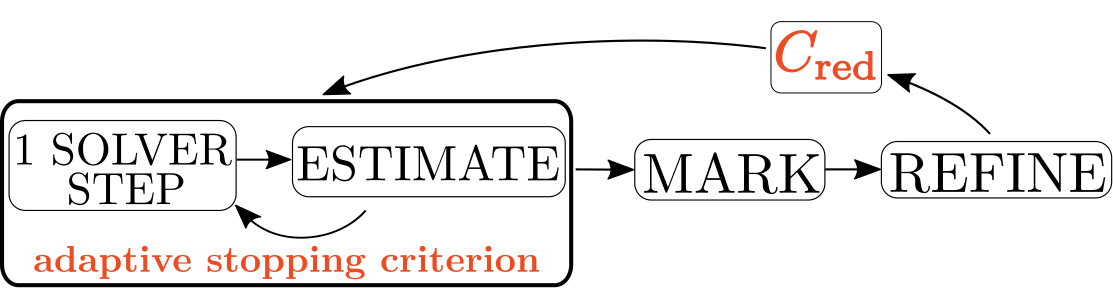
Keywords: equilibrated flux a posteriori error estimates, hp-adaptivity, finite element method, error reduction, algebraic error

Master thesis

Poster

We proposed a method for reconstruction of a single 3D object's surface from representative point cloud. Given the point cloud, we construct a triangular mesh approximation of a surface it represents. The reconstruction process is based on appropriately designed evolution of initial condition which is a simple triangular surface containing the point cloud in its inside. We establish a parabolic PDE prescribing the Lagrangian surface evolution and solve it numerically by a finite volume scheme. Throughout the whole evolution we perform a tangential redistribution of the mesh points in order to preserve the quality of the mesh. We applied the proposed method to the biological data representing an early developmental stage of zebra-fish embryo. The obtained results helped the biologists in quantitative analysis of the embryogenesis.

Examples of the obtained results on the cellular data:

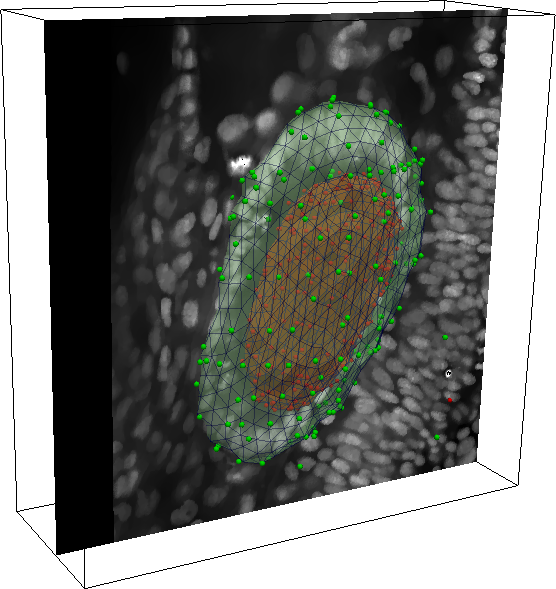
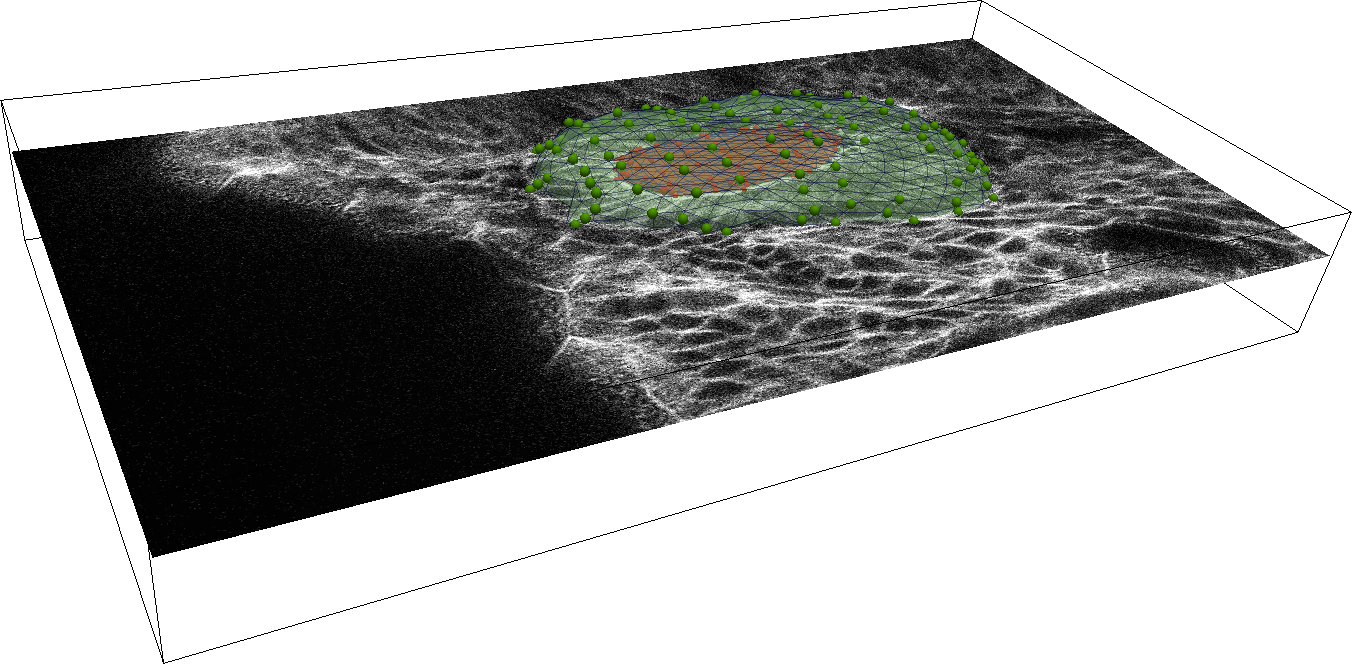
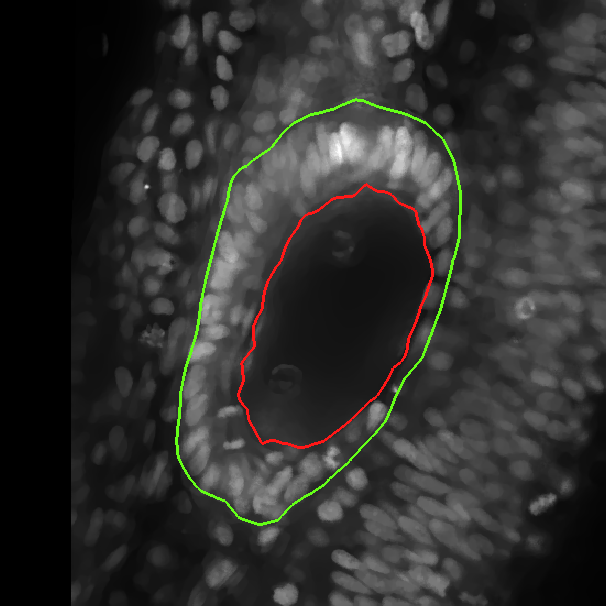
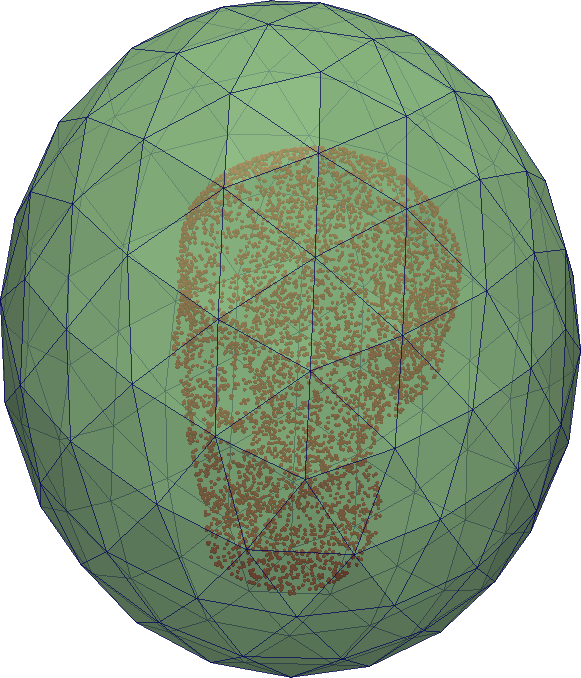
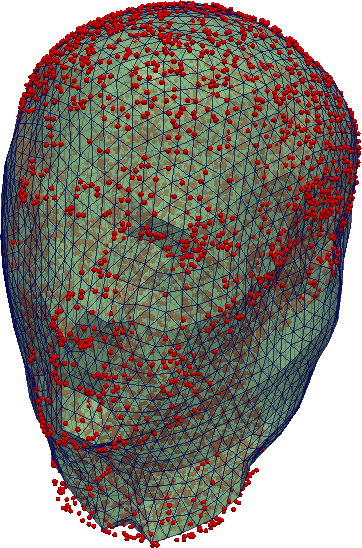
The results obtained with the test data:

Keywords: surface reconstruction, point cloud, surface evolution, tangential redistribution, finite volume method

Bachelor thesis

Within my bachelor thesis I studied the eigenvalues of the Laplace-Beltrami operator. We proposed a numerical method for solving the eigenvalue problem for this operator on 2D surfaces. For discretization of the operator we opted for a finite volume scheme. The obtained approximation of the spectrum of Laplace-Beltrami operator was then analyzed by multidimensional scaling algorithm in order to identify shape similarities. We applied the algorithm to real data which were the results of cell segmentation from microscope images of the embryo of the zebra-fish (danio rerio).

Examples of the obtained clusters of shape similar cells:

Keywords: Laplace-Beltrami spectra, finite volume method, shape analysis, multidimensional statistics, clustering