COALA

Our research focuses on a novel approach to dense and sparse linear algebra algorithms, which aims at minimizing the communication, where communication refers to both its volume and the number of messages exchanged. The main goal is to reformulate and redesign linear algebra algorithms so that they are optimal in an amount of the communication they perform, while retaining the numerical stability. In general, they reduce significantly the amount of time spent communicating, relative to conventional algorithms. The work here involves both theoretical investigation and practical coding on diverse computational platforms. The new algorithms are referred to as communication avoiding algorithms. 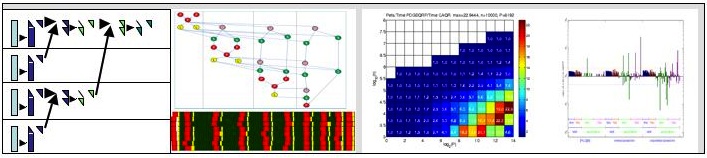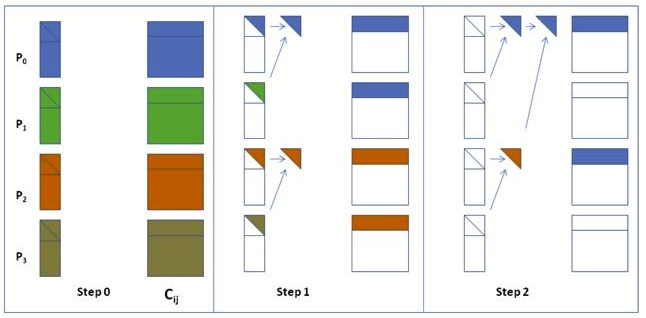Very often, they are based on a reformulation which expresses the operation on a block of columns of the input matrix as a reduce operation. The reduction tree influences the task dependency graph associated with the respective computation. Its choice depends on the underlying architecture.

Lower bounds on communication

Recent results have identified lower bounds on communication for direct operations (non Strassen like) in numerical linear algebra as LU and QR factorizations, eigenvalue and singular value computations. Most of the algorithms in the dense case that attain these bounds are new communication avoiding algorithms. In the sparse case, results to date have identified attainable lower bounds on communication for the Cholesky factorization of matrices arising from discretization on two dimensional and three dimensional regular grids. There are many open questions that are left in the sparse case. In particular, the simple operation of sparse matrix-matrix multiplication turns out to be more difficult to analyze than the Cholesky factorization.

Numerical Stability

Our goal is to design algorithms that are as stable as classic algorithms.
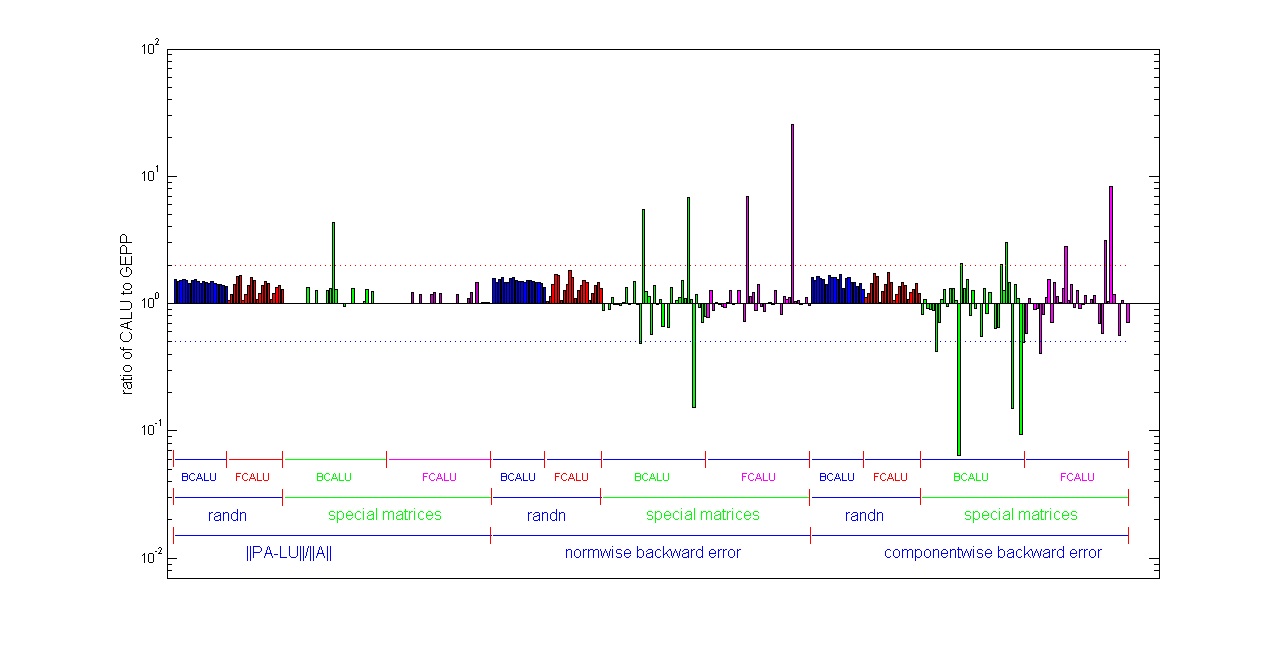
Communication avoiding LU (CALU) uses a new pivoting strategy, refered to as tournament pivoting. Our study of numerical stability includes proofs showing similarities between CALU and Gaussian elimination. In addition, extensive experimental results on random matrices and a set of special matrices show that in practice CALU is as stable as Gaussian elimination (see publication on CALU and figure on the left).
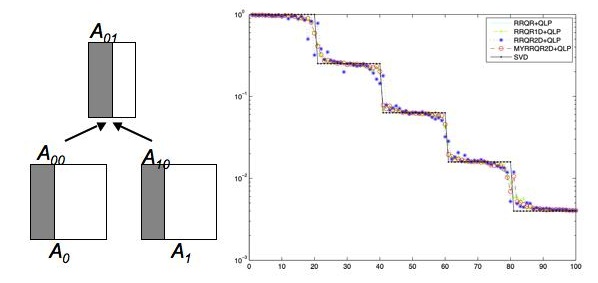
A similar tournamen pivoting technique is used in a communication avoiding rank revealing QR factorization. The results on the left show for the devil's matrix (a matrix with multiple gaps in the singular values) the values on the diagonal of L obtained after a QLP factorization.

Validation and Software

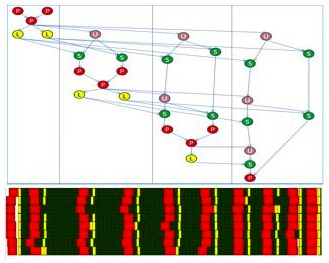The algorithms are implemented on hierarchical parallel machines based on SMPs of multicore processors. As in other related projects, as for example PLASMA, our approach consists in scheduling using dynamic or static techniques the task dependency graph of the associated communication avoiding algorithm. An important aspect that we consider in this collaboration is the validation of the algorithms in real applications, through our collaborations.