For a detail article on assessment of parameter identifiability through information theory, please see our article here. For an overview, please see below.

Information gain and entropy

In the context of parameter estimation of dynamical systems a reasonable question to ask is the following:

“How much information does one expect to gain about the parameters of interest through noisy measurements of an observable (or a set of observables) at a given set of discrete time instants?”

Such a question can be answered in the framework of information theory. The decrease in Shannon entropy (the continuous differential entropy) of the parameters by the availability of measurements can be used to quantify the information gain (see article here.).

A Windkessel example (ODE)

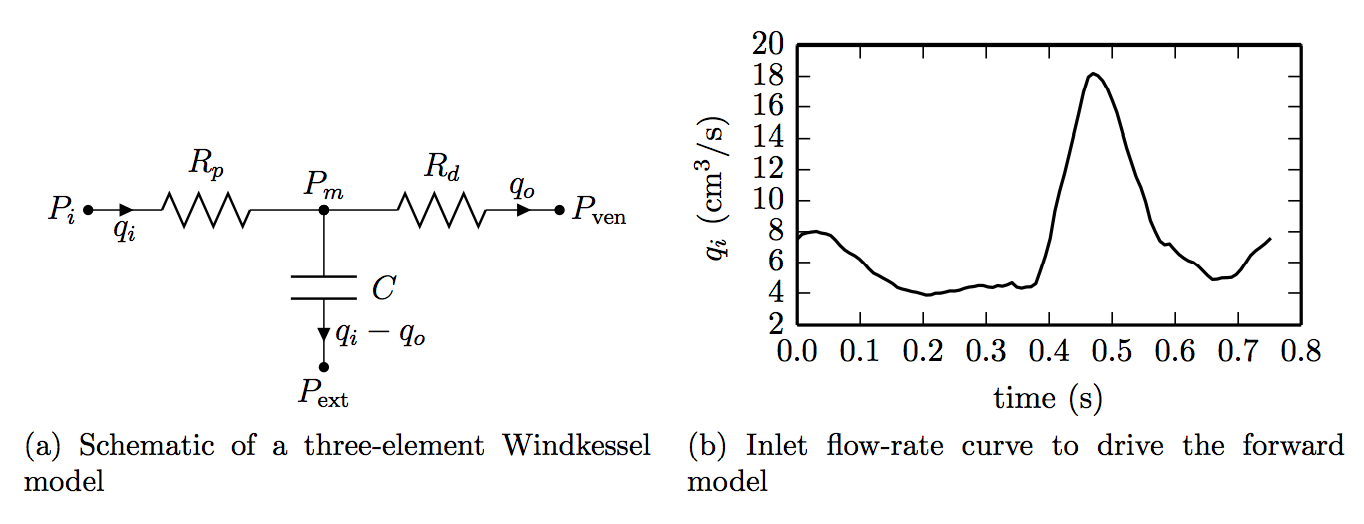
Figure 1: A three-element Windkessel model and the flow-rate curve

Parameter estimation in a three-element Windkessel model , a commonly imposed boundary condition to study haemodynamics, is considered. This model, as shown in Figure 1, consists of three elements: a proximal resistance, $R_p$, representing the sum of large vessels; a capacitance, $C$, representing the elastance of large vessels; and a distal resistance, $R_d$, representing the resistance of smaller vessels in the microcirculation. The behaviour of the Windkessel model of Figure [fig::RCR~s~chematic] is governed by the following differential algebraic equations

where $q_i$ and $q_o$ represent the inlet and outlet flow-rates, $P_i$ and $P_m$ represent the inlet and the mid-Windkessel pressure, and $P_\text{ven}$ and $P_\mathrm{ext}$ represent the venous and external pressures, respectively. $P_\mathrm{ven}$ and $P_\mathrm{ext}$ are both assumed to be zero. The inlet flow-rate, the control curve, is known and is shown in Figure 1. The goal of this analysis is to determine the identifiability of the Windkessel parameters ($R_p$, $C$, $R_d$) by discrete measurements of $P_i(t)$

where $\tilde{z}(t_j)$ represents the measurement of $P_i(t_j)$ at time $t_j$, and $\tilde\epsilon(t_j)$ represents the associated measurement noise.

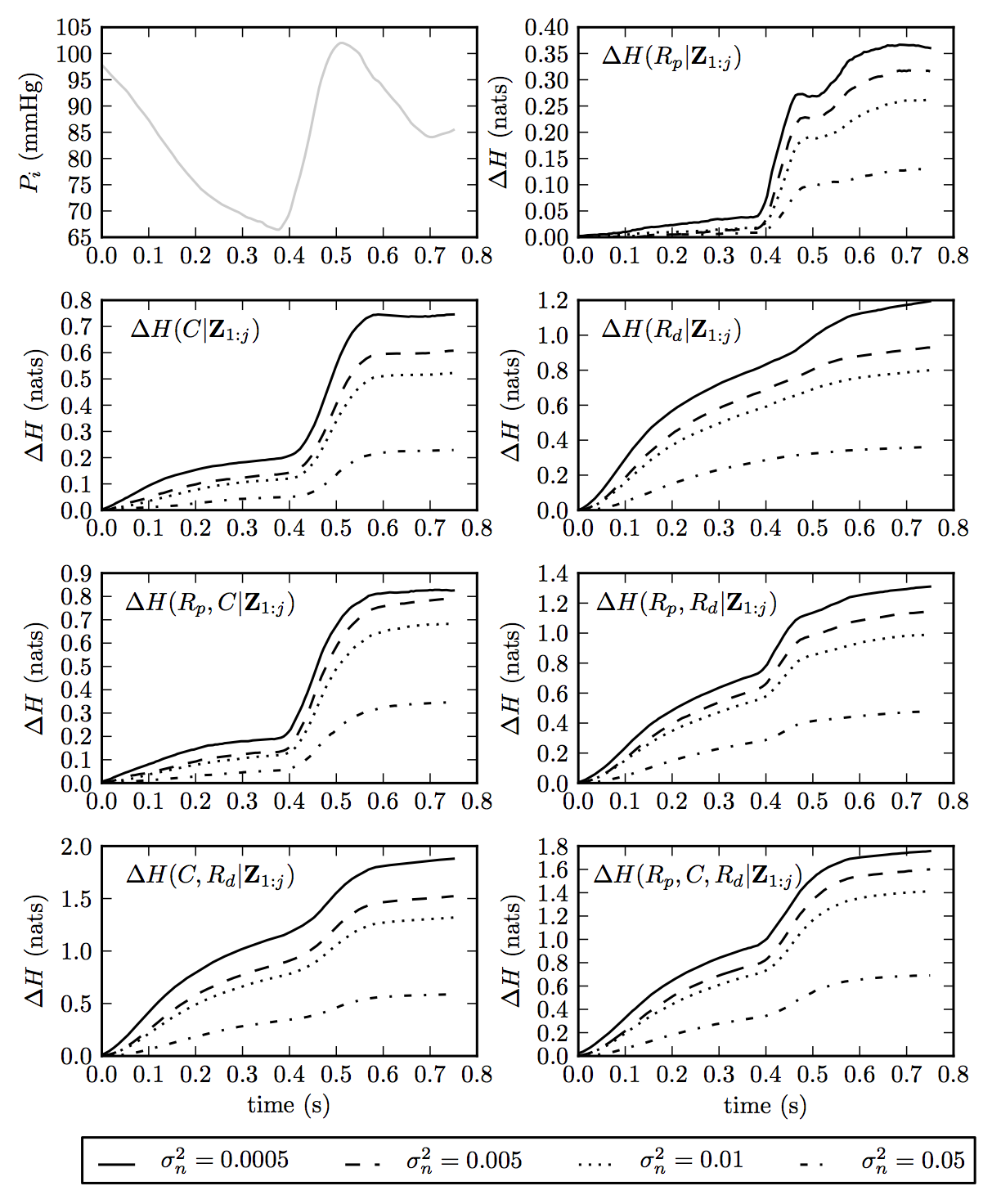
Figure 2: Gain in information for various parameter combinations in the Windkessel model. For $σ_n^2$ = {0.0005, 0.005, 0.01, 0.05}, the corresponding variances of the noise process for the real parameter $P_i$ are {1.8, 17.8, 35.7, 183.7} mmHg$^2$

The expected information gains for individual parameters, pairs of parameters considered together, and the triplet consisting of all the three parameters, are shown in Figure 2. From the relative magnitudes of expected information gains for the individual parameters it can be concluded that $R_d$ is most easily identifiable (largest gain in information) while $R_p$ is most difficult to identify (lowest gain in information). Furthermore, it is observed that most of the information about the parameter $R_p$ is contained in the sharp systolic phase of pressure ($t \in [0.4,0.5]$). The effect of increasing noise in Figure 2 is consistent with the intuition that a higher noise should result in a lesser amount of information gain.

For a detail analysis and interpretation see article here.

Advection-Difffusion equation in 2D.

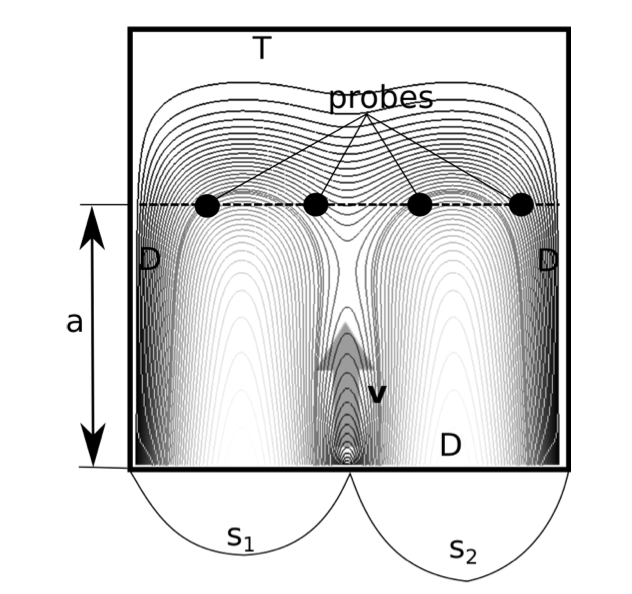
This example is a system governed by a $2+1$ dimensional PDE, that is aimed to mimic a source detection inverse problem for an advection-diffusion equation (see Figure 3). A physical point domain is $(\boldsymbol{\xi},t) = (\xi_1,\xi_2,t)\in \Omega = [0,1]^2 \times [0,0.1]$, where $\xi_1$ and $\xi_2$ are the horizontal and vertical coordinates respectively. The system unknown is a passive scalar $c$ that diffuses and is simultaneously advected by a velocity $\mathbf{v}$.

The equation governing the dynamics reads:

where $S(\xi_1)$ is the source function, defined by:

Figure 3: Advection-diffusion model: the domain is the unit square, the probes are located at $y=a=0.6$. The capital letter $D$ corresponds to Dirichlet boundary conditions while $T$ are transparent boundary conditions. The velocity is mostly aligned with the $\xi_2$ axis. The function that mimics the source is characterised by two parameters $s_{1,2}$. Superimposed, the contours of the solution at $t = 5\ 10^{-2}$ normalised, 40 values between the maximum and the minimum. The parameters to obtain this solution are: $s_1,s_2 = 25$, $v_1 = 0$, $v_2 = 10$, $\mu = 0.1$.

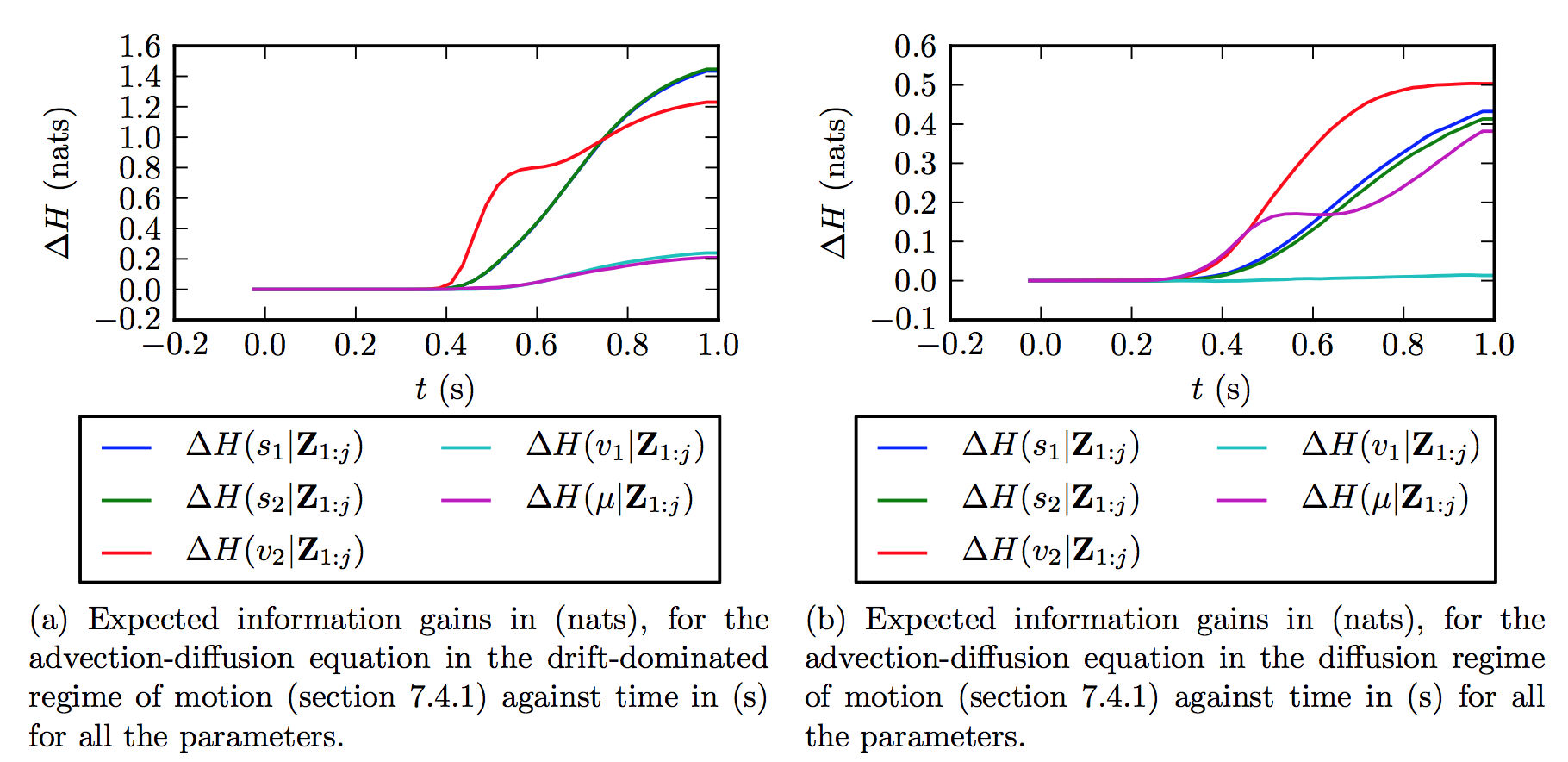
The goal of the study is the identifiability of the parameters $s_1, s_2, \mu, v_1,$ and $v_2$ (where $v_1$ and $v_2$ are the components of the drift velocity) by measuring the concentration at the probe locations. Two different scenarios are investigated: a drift regime and a diffusive regime. Figure 4 shows the expected information gains in these regimes.

Figure 4: Information gains for the advection-diffusion problem (section references are to the article here.)

Drift Dominated Regime In this regime, intuitively, owing to low diffusion, the information about the sources is transported downstream relatively unadulterated to the probes. From Figure 4, it can be seen that the source intensities are well identifiable. The less identifiable parameters are the diffusivity $\mu$ (which is quite small in the drift-dominated regime) and the horizontal velocity $v_1$.

Diffusion Dominated Regime Here, the passive scalar dynamics is dominated by diffusion The sources are still individually identifiable. However, the gain in information about the source intensities is much less when compared to the drift-dominated case.

Even if in both cases the source intensities are mathematically identifiable in a noiseless setting, there is a difference from a pragmatical standpoint. In the presence of noise, when different regimes of motion are considered, the information learned about the parameters can vary significantly.

For a detail analysis and interpretation see article here.