Le but du TD est de commencer à manier les graphes et de mettre en pratique le parcours en profondeur dans la recherche des composantes connexes. Le minimum à faire en deux heures sont les exercices 1 et 2. Il est recommandé de plus d'avoir fait les exercices 3 et 4. L'exercice 5 est d'une difficulté supérieure.
A la fin du TD, vous devez déposer vos programmes en tapant dans une fenêtre xterm une commande :
/users/profs/info/Depot/INF_431/deposer [pgm] TD_1 [gpe]
où [pgm] doit être remplacé par la liste des
noms des fichiers
contenant vos programmes et [gpe] doit être remplacé par
votre numéro de groupe. Par exemple, pour déposer des fichiers
Liste.java et Graphe.java qui sont dans
le répertoire courant, un élève du groupe 18 doit taper :
/users/profs/info/Depot/INF_431/deposer Liste.java Graphe.java TD_1 18
Le but du jeu est de passer d'un mot à un autre par une suite de mots
tels qu'un mot et le suivant ne diffèrent que d'une lettre. Par
exemple, on peut passer de lion à
peur par la suite de mots :
lion pion paon pain paix poix poux pour peur
Nous allons modéliser ce jeu par un graphe deux mots sont reliés s'il ne différent que d'une lettre. Une suite de mot telle que ci-dessus est donc un chemin dans le graphe. L'ensemble des mots auxquels peut mener un mot constitue une composante connexe.
On appellera successeurs d'un mots les mots qui ne
différent que d'une lettre de ce mot. Par exemple, les successeurs de
lion sont pion et lien, ceux de
lien sont rien, bien,
sien, lieu, lier,
lied, lion, tien et
mien.
Nous allons définir un graphe par un tableau mot qui
contient l'ensemble des mots de départ et un tableau
listeSucc de listes d'entiers qui contiendra les listes
de successeurs. Un mot est repéré par son indice i dans
le tableau mot. listeSucc[i] contiendra la
liste des indices des mots reliés à mot[i]. Pour
faciliter l'écriture du programme, il est utile de stocker le nombre
de mots dans une variable nb.
Écrire une classe Liste pour manier des listes
d'entiers, puis une classe Graphe avec un constructeur
Graphe (String[] lesMots) qui initialise les variables
ci-dessus avec des listes de successeurs vides.
Écrire une méthode static void ajouterArete (Graphe g, int s,
int d) qui rajoute s à la liste des successeurs de
d et d à celle de s, les mots
d'indices s et d étant supposés différer
d'une lettre.
Écrire une méthode static void lettreQuiSaute (Graphe
g) qui initialise les listes de successeurs selon la règle du
jeu de la lettre qui saute. On pourra utiliser la fonction suivante
qui renvoie true quand deux chaînes de même longueur
diffèrent d'une lettre :
static boolean diffUneLettre (String a, String b) {
// a et b supposees de meme longueur
int i=0 ;
while (i<a.length () && a.charAt (i) == b.charAt (i))
++i ;
if (i == a.length ()) return false ;
++i ;
while (i<a.length () && a.charAt (i) == b.charAt (i))
++i ;
if (i == a.length ()) return true ;
return false ;
}
Vous pouvez tester vos méthodes avec la fonction main
suivante :
public static void main (String[] args) {
String[] dico3court = { "gag", "gai", "gaz", "gel", "gks", "gin", "gnu", "glu", "gui", "guy", "gre", "gue", "ace", "acm", "agi", "ait", "aie", "ail", "air", "and", "alu", "ami", "arc", "are", "art", "apr", "avr", "sur", "mat", "mur" } ;
Graphe g = new Graphe (dico3court) ;
lettreQuiSaute (g) ;
//afficher (g) ;
}
Écrire une méthode afficher qui permet d'afficher
le graphe de la manière suivante :
graph dico {
node [color=red, fontcolor=black, fillcolor=white, style=filled]
edge [len=1.1, style=bold, color=blue]
gag -- { gaz gai }
gai -- { gui gaz gag }
gaz -- { gai gag }
gel -- { }
...
}
Le format est celui de graphviz (une suite de logiciels
pour visualiser des graphes), les trois premières lignes
et la dernière peuvent être reprises telles quelles (elles servent
principalement à indiquer la couleur des arêtes et des noeuds,
len=2 au lieu de len=1.1
permet d'allonger les arêtes).
Les commandes
neato et dotty permettent ensuite
de visualiser le graphe avec par exemple :
java Graphe | neato | dotty - (avec un moins à la
fin) qui donne :
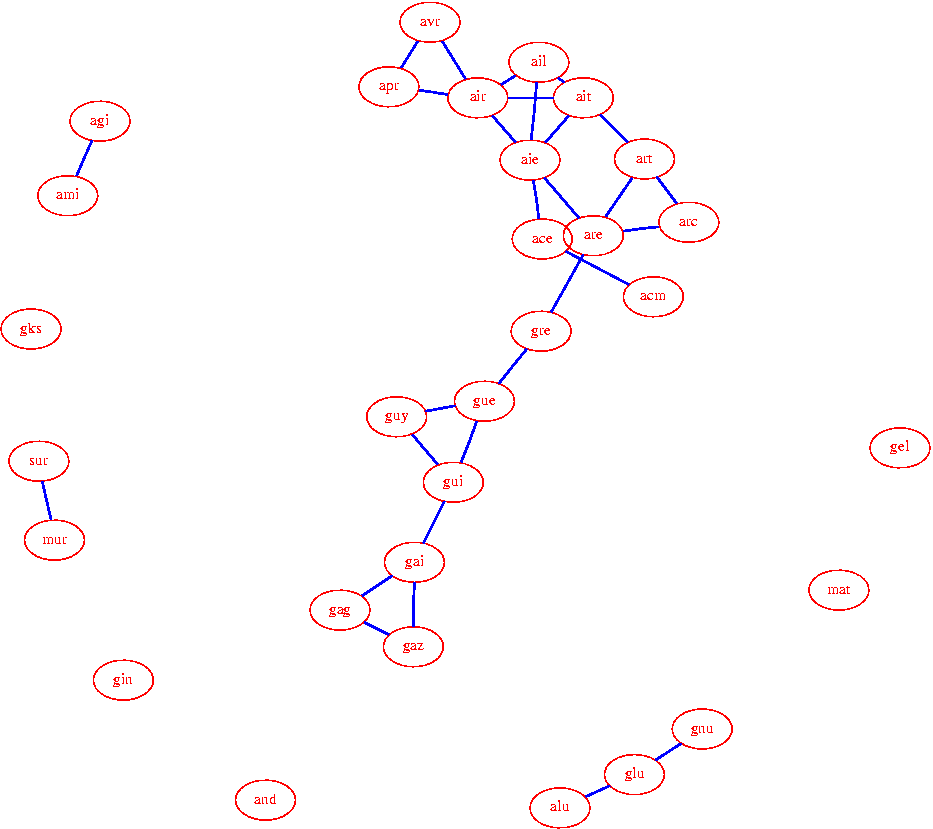
Pour plus d'information sur graphviz, vous pouvez essayer la
commande man dot. En résumé, dot calcule
un plongement dans le plan d'un graphe orienté (syntaxe générale
du type digraph nomGraphe { noeud1 -> noeud2 ; nomNoeud -> autreNomNoeud ; ...}) et neato calcule un plongement dans le plan
d'un graphe non orienté (syntaxe générale
du type graph nomGraphe { noeud1 -- noeud2 ; nomNoeud -- autreNomNoeud ; ...}). dotty sert ensuite à visualiser le résultat à l'écran
(dotty ne lit pas l'entrée standard à défaut d'autre argument,
il faut pour cela lui donner - (moins) comme argument.)
La classe Dico.java contient les
tableaux des mots de 3, 4 et 5 lettres (Dicos.dico3,
Dicos.dico4, Dicos.dico5). Il peut y avoir des
doublons, mais on essaiera pas de les traiter (plusieurs sommets du graphe
risquent donc de correspondre au même mot s'il apparaît plusieurs fois
dans le dictionnaire).
Le but est maintenant de calculer les composantes connexes grâce à un parcours en profondeur.
Pour faire un parcours en profondeur, nous avons besoin de stocker
pour chaque mot d'indice i s'il a déjà été rencontré.
On utilisera pour cela un tableau de boolean
de nom dejaVu.
Rajouter les variables nécessaires dans la classe Graphe, et modifier le constructeur en conséquence.
Écrire une fonction static void dfs (Graphe g, int x)
qui parcourt en profondeur le graphe g à partir du mot
d'indice x. Pour mémoire, cela veut dire qu'on marque
x comme déjà vu et que l'on inspecte un à un les mots de
sa liste de successeurs. Si un successeur d'indice y
n'est pas marqué comme déjà vu, on parcourt récursivement ce mot, on
dit alors qu'il a été vu par le mot d'indice x.
Pendant toute la durée de l'appel à dfs (g, x), on dit
que l'on est en train de visiter le mot d'indice
x.
Modifier la fonction de sorte que tous les mots vus durant la
visite du mot d'indice x soit affichés.
Écrire une fonction static void visit (Graphe g) qui
initialise dejaVu, puis qui parcourt en profondeur tout
le graphe. Pour mémoire, cela veut dire qu'on prend un mot non encore
vu, qu'on parcourt en profondeur à partir de ce mot et qu'on
recommence jusqu'à ce que tous les mots aient été vus.
Faire en sorte que les
composantes connexes soient affichées. Avec les mots de
dico3court, on doit trouver 9 composantes :
1: gag gaz gai gui gue gre are art arc ait air avr apr ail aie ace acm guy 2: gel 3: gks 4: gin 5: gnu glu alu 6: agi ami 7: and 8: sur mur 9: mat
Trouver la composante connexe de lion et
peur parmi les mots de 4 lettres qui sont listés dans le
tableau Dicos.dico4 de Dicos.java.
Le but est maintenant de calculer un chemin d'un mot à un autre s'il en existe un.
Lors d'un parcours en profondeur, si lors de la visite d'un mot
d'indice x, un successeur d'indice y est vu
par x, on peut définir x comme le père de
y. On obtient alors une arborescence de Trémaux.
Rajouter dans la classe Graphe une variable
pere qui permettra de stocker pour le mot d'indice
i, l'indice pere[i] de son père dans
l'arborescence.
Modifier le constructeur et les deux fonctions de parcours en profondeur pour intégrer le calcul de l'arborescence de Trémaux.
Modifier le programme pour qu'il prenne deux mots en arguments et
affiche une suite de mots menant de l'un à l'autre si c'est possible.
Écrire pour cela une fonction static void chemin (Graphe g,
String from, String to) qui affiche un chemin de
from à to s'il en existe un. On pourra
utiliser la fonction suivante qui retrouve l'indice d'un mot
m dans un tableau de mots tabMots :
static int indice (String m, String[] tabMots) {
for (int i=0 ; i<tabMots.length ; ++i)
if (m.equals (tabMots[i])) return i ;
throw new Error (m + " n'est pas dans le tableau.") ;
}
Trouver de cette manière un chemin de lion à
peur.
Écrire une fonction static void dfsIteratif (Graphe g, int
x) qui fait un parcours en profondeur à partir du mot d'indice
x de manière itérative (sans appels récursifs). On
utilisera pour cela une pile contenant les indices des mots restant à
visiter.
Écrire une fonction static void bfsIteratif (Graphe g, int
x) qui fait un parcours en largeur à partir du mot d'indice
x. Dans un parcours en largeur, on visite d'abord tous
les successeurs et ensuite les successeurs des successeurs non encore
visités et ainsi de suite. Les premiers successeurs rencontrés
seront visités en premier, il est donc utile d'utiliser une
file "first in first out".
Modifier la fonction chemin de l'exercice 3 pour
qu'elle trouve un plus court chemin plutôt qu'un chemin quelconque.
Vous trouverez tous les mots du dictionnaire dans
tout.dicofrancais. Il contient un mot par ligne dans un ordre quelconque.
Le graphe est orienté et défini par deux paramètres sup
et dif. Il y a un arc d'un mot u
vers un mot v quand v peut être obtenu
à partir de u en supprimant au plus sup
lettres et en changeant au plus dif. (Le calcul du graphe
doit se faire en moins de 10 minutes pour sup=1
et dif=1.)
L'excentricité d'un mot u est la longueur
maximale d'un plus court chemin de u vers un autre mot.
Trouver un mot d'excentricité maximale et découvrir ainsi
un plus court chemin le plus long possible du graphe.