Differential and Algebraic Riccati EquationS
Explicit H∞ controllers for 4th order
single-input single-output systems with
parameters and their application to the two
mass-spring system with damping.
The following pictures and/or animations are sections of the algebraic surface defining necessary and sufficient conditions on the unknowns that parameterize the admissible formal solutions of the associated Algebraic Ricatti Equation. We plot below lambda=gamma^2-1 in function of the reduced system parameter rho, where gamma is the H∞ criteria which measures the maximal robustness of the closed-loop system of the two mass spring dampler system
The same simulation but setting directly Gamma (G on the picture) as vertical axis:
Again the same simulation but after compactifications to one point (Xi = (gamma-1)/(gamma+1) , nu0 = Gr/(Gr+1) and nu1 = rho/(rho+1)):
Numerical instability. As it could be easily noticed, this surface is numerically unstable : for example, implicitplot function from Maple computes the following picture :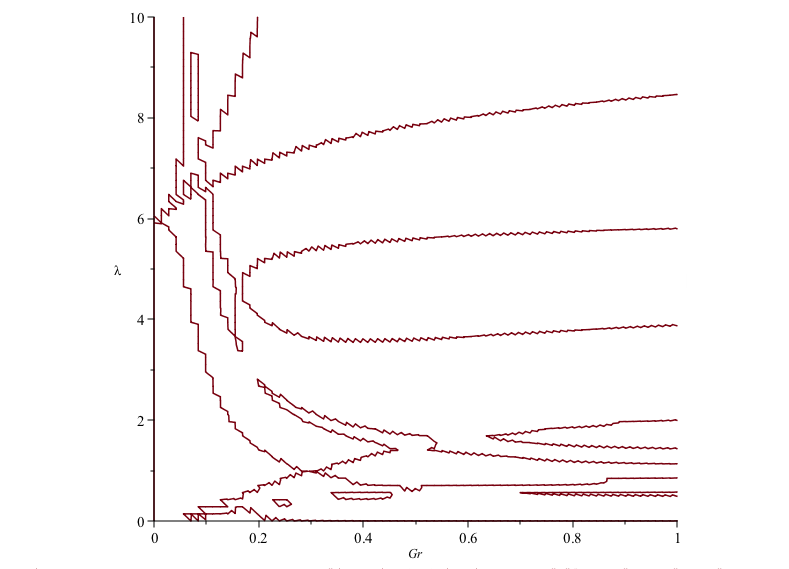
One can observe that simply taking an approximation of the section rho=1/10 with 10 digits of precision will give the following curve ( certified drowing ) :
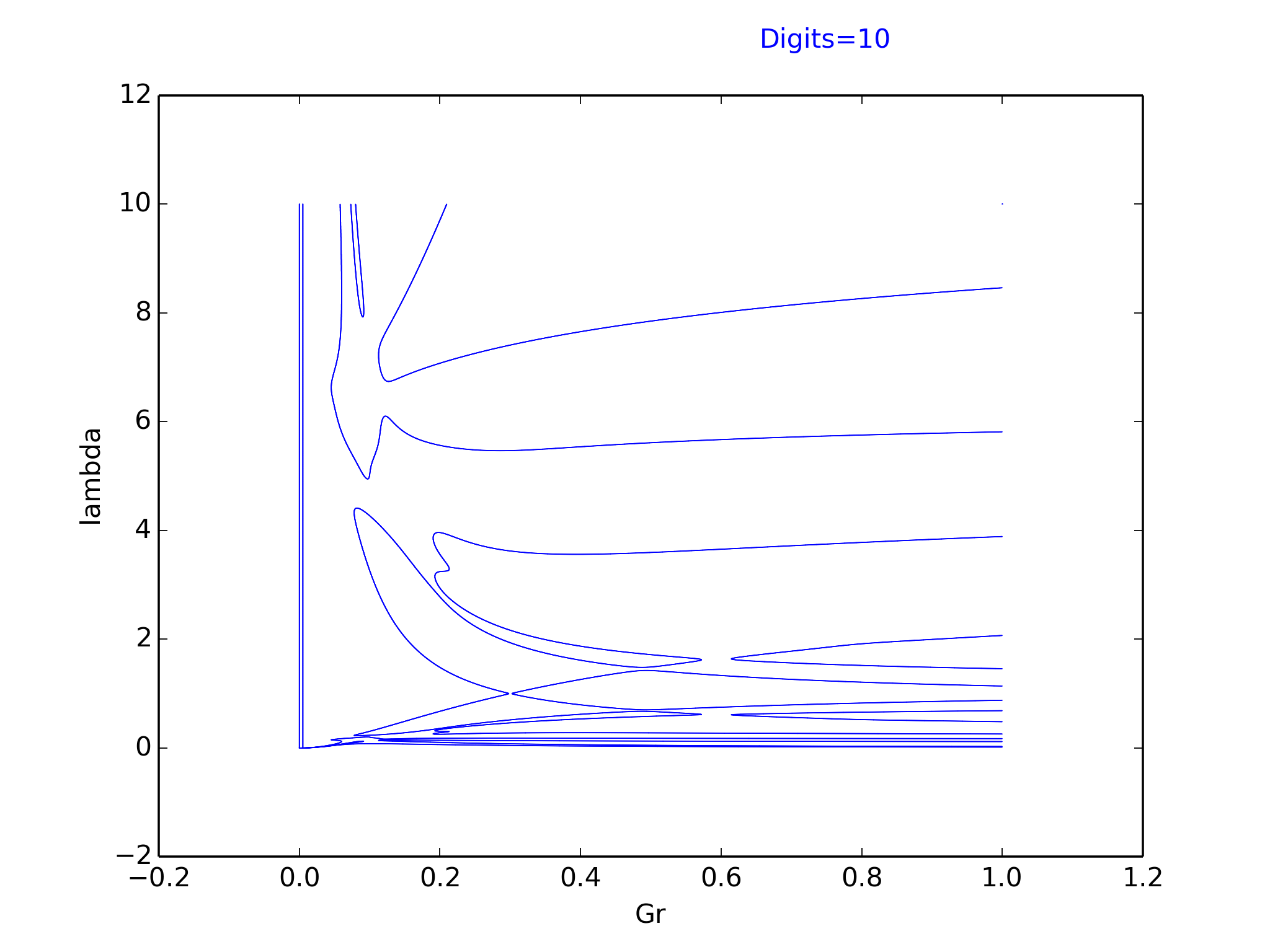
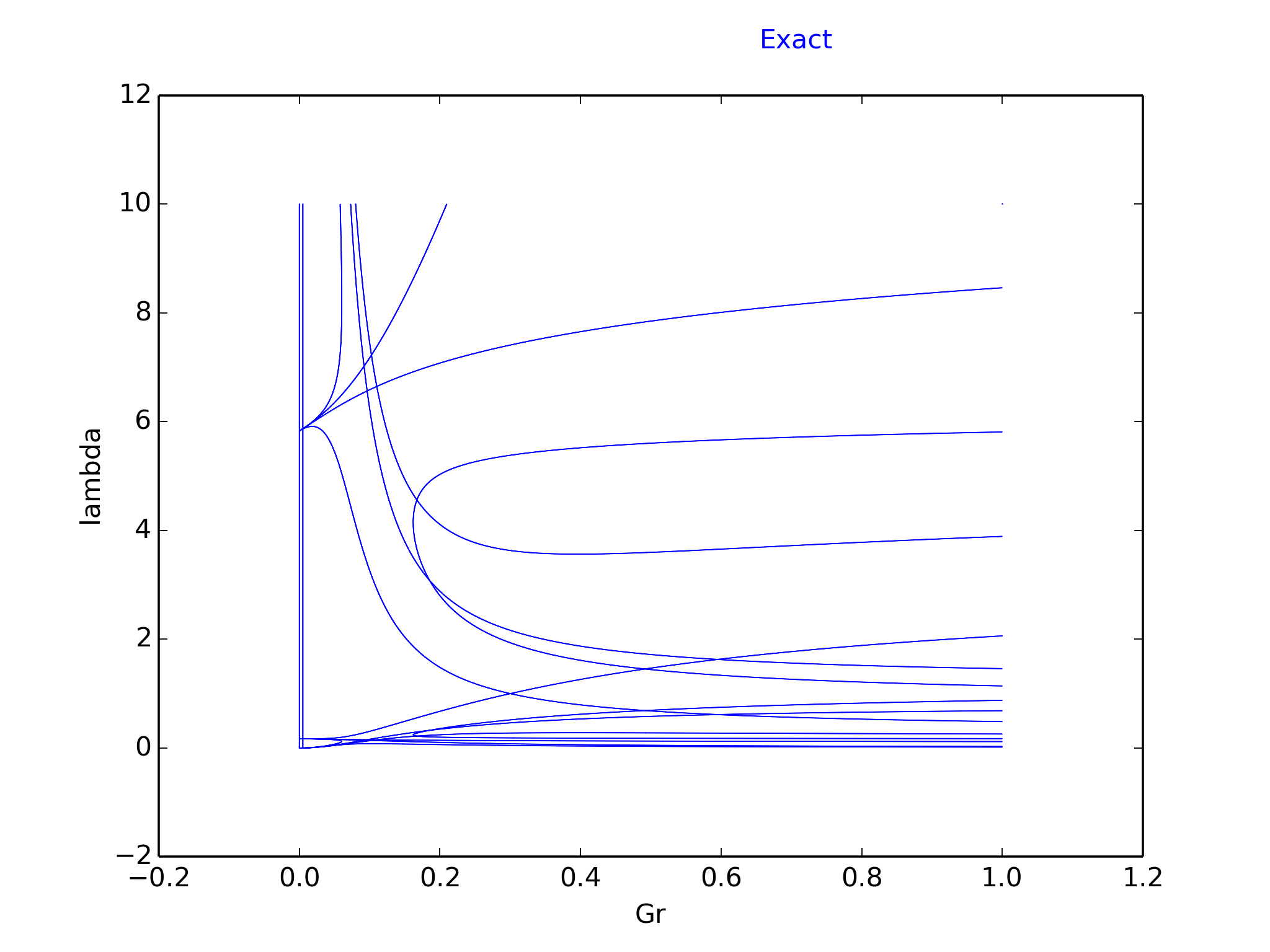
while performing the same computation using rational numbers will give the following curve ( certified drowing ) :
The following pictures and/or animations are sections of the algebraic surface defining necessary and sufficient conditions on the unknowns that parameterize the admissible formal solutions of the associated Algebraic Ricatti Equation. We plot below lambda=gamma^2-1 in function of the reduced system parameter rho, where gamma is the H∞ criteria which measures the maximal robustness of the closed-loop system of the two mass spring dampler system

The same simulation but setting directly Gamma (G on the picture) as vertical axis:

Again the same simulation but after compactifications to one point (Xi = (gamma-1)/(gamma+1) , nu0 = Gr/(Gr+1) and nu1 = rho/(rho+1)):

Numerical instability. As it could be easily noticed, this surface is numerically unstable : for example, implicitplot function from Maple computes the following picture :

One can observe that simply taking an approximation of the section rho=1/10 with 10 digits of precision will give the following curve ( certified drowing ) :

while performing the same computation using rational numbers will give the following curve ( certified drowing ) :

Certified drawing. We make use of the
bivariate solver described in [1] for computing
an exact parameterization of
the x-critical, y-critical and singular points of the
curve and combine this with the interval
arithmetic variant of the root isolator from [2]
to certify each pixel of the drawing : a
pixel lights if and only if the curve cross
it.
- [1] Bouzidi, Y., Lazard, S., Moroz, G., Pouget, M., Rouillier, F. and Sagraloff M. Improved algorithms for solving bivariate systems via Rational Univariate Representations, 2016, Journal of Complexity.
- [2] Rouillier, F. and Zimmermann, P. Efficient Isolation of Polynomial Real Roots, 2003, Journal of Computational and Applied Mathematics, Vol. 162(1), pp. 33-50